Precognitive Dreams: Bifurcations Due to Tolerance of Ambiguity and Dream Frequency

What Precognitive Dreams are Made of: The Nonlinear Dynamics of

Tolerance of Ambiguity, Dream Recall, and Paranormal Belief [1]

Rense Lange

Illinois State Board of Education

Michael Schredl

Central Institute of Mental Health

James Houran

Southern Illinois University School of Medicine

Abstract

Using a framework derived from nonlinear dynamics, two studies investigated a cusp model of precognitive dreaming using the GEMCAT II software for catastrophe estimation. As predicted, Study I (N = 50) and Study II (N = 59) both indicated that tolerance of ambiguity and dream recall loaded significantly on the cusp’s latent bifurcation variable (Y), whereas belief in the paranormal functioned as an asymmetry variable (X) (all p < .05). The validity of the proposed model is supported by the findings that a competing linear model, as well as an alternative cusp formulation in which the roles of the X and Y indicators were reversed provided a significantly poorer fit to the data in both experiments (p < .001) than the hypothesized cusp formulation. The differential fit of the three models is reflected both in the models’ (Pseudo-) R² values and via standard non-parametric tests over the models’ squared residuals. The findings support the hypothesis that some experiences of precognitive dreams (represented by the statement “There have been events that I dreamed about before the event occurred”) are illusions, i.e., coincidences between the contents of dreaming and waking experience that are noticed due to frequency of dream recall and given credence due to the combined effects of belief in the paranormal and a tolerance of ambiguity.

Keywords: precognitive dreams, cusp catastrophe, tolerance of ambiguity, belief in the paranormal, GEMCAT II

A precognitive dream is defined as a dream that seemingly includes knowledge about the future which cannot be inferred from actually available information (Stowell, 1995). Precognitive dreams have been reported throughout history; famous examples are the pharaoh’s dream of seven fat and seven meager cows (Hendricks, 1989) and Bishop Lanyi’s dream of the assassination of Archduke Franz Ferdinand at the beginning of World War I (Clericus, 1918). Although the phenomenon is often considered “paranormal” it occurs quite frequently:17.8 % to 38 % persons of large samples of individuals reported that they experienced at least one precognitive dream (Palmer, 1979; Haraldsson, 1985; Ross & Joshi, 1992; Thalbourne, 1994). Most studies indicate that women report more precognitive dreams than men, while the frequency of precognitive dreaming declines with age. The percentage of persons who believe that precognitive dreaming is possible is even larger, and estimates range from 63 % to 98 % (Thalbourne, 1984; Haraldsson, 1985).

Table 1: Criteria for precognitive dreams (Bender, 1966)

Criteria

1.Dream must be told or recorded before its fulfillment

2.Dream must include enough details to render chance fulfillment unlikely

3.The possibility of interference from actual knowledge must be excluded

4.Self-fulfilling prophecies must be excluded

5.Telepathic influences can not explain the occurrence of the precognitive dream

Despite the frequent occurrence of precognitive dreaming, scientific exploration of the phenomenon faces a number of issues. First, most spontaneously occurring precognitive dreams do not fulfill the criteria depicted in Table 1 which are necessary to differentiate precognitive dreaming from other phenomena such as deja vu experiences, telepathic dreams, memory distortions and merely chance occurrences. Besterman (1933) found that only two out of 45 reported precognitive dreams (4.4 %) met these criteria, i.e., the high prevalence rates which were obtained by questionnaires using items such as “Do you have dreams that later come true?“ may be an overestimation in comparison to the occurrence of precognitive dreams fulfilling the criteria of Table 1. While arguably all experiences of precognitive dreams are subsumed by this question, so are instances of non-precognitive type dreams. For instance, an individual could be dreaming about a dentist appointment to occur the next morning due to the ensuing anxiety. However the use of this general question can help in constructing theoretical models that can be tested later when more precise measures of precognitive dreaming are developed. Secondly, given the experimental evidence for psi (e.g., Bem & Honorton, 1994; Radin, 1997)[2], researchers face the problem that strong support for the precognition hypothesis challenges many people’s fundamental world views regarding causality. Thus, Mischo’s (1985) observation that support for this hypothesis can elicit anxieties seems very plausible. Third, the verification of a theory is according to the critical rationalism not possible (Popper, 1978), i.e., even a large amount of supportive evidence (confirmed examples of precognitive dreaming) cannot prove the theory. Of course, this problem concerns theory testing in general (Meehl, 1978).

In view of the methodological issues raised above, three approaches have been applied to the investigation of precognitive dreams: investigating spontaneously occurring precognitive dreams, diary studies and experimental studies.

Spontaneously Occurring Precognitive Dreams

Large surveys of spontaneous cases (Rogers, 1923; Saltmarsh, 1934; Rhine, 1954; Hearne, 1984; Ryback & Sweitzer, 1990) have shown that the themes of precognitive dreams are mostly negative, e.g. death of a relative, one’s own death, natural disaster, war and accidents. Stevenson (1961) and Stowell (1997a, b) reported that these dreams are vivid, intense and have a personal significance for the dreamer. Schriever (1987), however, analyzed 115 dreams of a single subject and found no differences between well confirmed precognitive dreams (see Table 1) and insufficiently confirmed dreams regarding emotional intensity, vividness and personal significance. Therefore, the preponderance of negatively toned precognitive dreams may be explained by the bias that persons reported solely impressive cases to the researcher. This is comparable to the emotions of ordinary dreams since surveys eliciting dreams retrospectively found a preponderance of negative dreams whereas diary studies or laboratory awakenings yielded a balanced ratio between positive and negative dream emotions (Schredl & Doll, 1998). Since the researcher cannot investigate the spontaneous precognitive dream of an event after its occurrence, in-depth inquiries (see Table 1) are often not possible. Barker (1967), for example, placed a newspaper announcement looking for precognitions about the Aberfan disaster (where 144 persons were killed) and found that only 3 out of the 76 responses met the criteria in Table 1. A similar study was conducted by Murray and Wheeler (1937). After the kidnapping of the Lindbergh baby, they published a newspaper request throughout the country which yielded over 1300 dreams prior to the discovery of the baby’s body. Only seven dreams contained several general details (e.g. location in a wood, buried) matching with the actual circumstances of the baby’s death. These authors questioned the possibility of precognition.

A major problem of this kind of research is the lack of control samples to estimate the base rate of such dream themes. Yet, despite the methodological problems inherent to this approach, it seems valuable to investigate spontaneous cases in the future; not as evidence but as material which contributes to the theorizing about the phenomenon.

Diary Studies

During a dream diary study the participants record their dreams every morning upon awakening (thereby fulfilling criterion 1 of Table 1) and they are instructed to compare subsequent waking events to the dream content (Dunne, 1927; Besterman, 1933; Bender, 1966; Schriever, 1987; Sondow, 1988). This approach, which elicits a larger number of precognitive dreams per participant than spontaneous cases, indicates that precognitive dreams are not dominated by negative emotions (Schriever, 1987). Sondow (1988) analyzed 96 precognitive dreams (out of a series of her own 943 dreams) and found that there is an exponential relationship between the occurrence of a precognitive link and the time interval between dream and the actual waking event (cf. Green, 1960; Orme, 1974; de Pablos, 1998). About 41 % of the precognitive dreams were linked to an event of the following day (Sondow, 1988). To rule out the possibility of memory artifacts, Sondow (1988) compared a period with intense re-reading of the dreams in order to match them to subsequent events to a period without re-reading the dreams. In both cases she found an exponential decrease as a function of the time interval, but significantly more matches were found in the re-reading period. This supports the hypothesis that memory factors play a crucial role, i.e. the participants have to keep the dream in mind in order to find links to waking events.

Interestingly, dream research has revealed a similar pattern (exponential decline) for the temporal references of dream elements (e.g. Botman & Crovitz, 1989-90). The hypothesis of Dunne (1927) and Jackson (1967) that references to future events occur as often as references to past events is not supported by empirical data since about 10 % of dreams were found to be precognitive (Besterman, 1933; Bender, 1966; Sondow, 1988), whereas for 25 % to 75 % of the dream elements references to past events were detected (Strauch & Meier, 1996). Although research has shown that dream content is affected by the study’s design (cf. Schredl, 1999a), no systematic investigation has been carried out to test whether intense looking for matches between waking life and dreams changes dream content. It seems plausible, however, that the extensive reading of newspapers affects dream content such that people dream more about global events, thereby heightening the chances for future matches.

Jackson (1967) observed that the procedure of connecting dream elements with subsequent waking events by the participants does not allow an estimation of chance coincidences. Therefore, he suggested a two-group design. Group A keeps a dream diary over a one-week period and is then exposed to a special waking experience (unusual for all participants) and records another week their dreams. Group B also keeps dream diaries over two weeks but they are not exposed to the special waking experience. The advantage of this controlled design is the possibility to estimate the effect of the unusual experience on subsequent dreams, using the contents of the dreams of group B as a base rate. Laboratory studies (see next section) and a few diary studies have partly applied Jackson’s suggestions. In Hearne’s (1986) study, two independent judges rated possible links between 52 dreams of a single subject to newspaper reports of the following 28 days. To control for chance coincidences newspaper reports of the previous and following year were included. Statistically significant correspondences were found and some dream reports showed striking matches (Hearne, 1986). Harley (1989) utilized 20 sets of four pictures from which one picture was chosen by random selection procedures. The participants were asked to choose – according to their dreams – the picture that would be selected. Harley (1989) obtained a significant psi-missing effect, i.e. target pictures were less often chosen than non-target pictures. Sixty-eight dream reports of 23 participants were gathered by Emery (1991) who asked her participants to dream about the cover of the magazine “Newsweek” which would be published two weeks ahead. Although Emery (1991) obtained 11 good matches, her results have to be interpreted with caution since no control condition was introduced.

Experimental Laboratory Studies

The research group at the Maimonides hospital in New York carried out studies on telepathy and dreaming (Ullman, Krippner & Vaughan, 1977) and two studies on precognitive dreams (Krippner et al., 1971; 1972). Participant in both studies was Malcolm Bessent, an English “sensitive” with a history of reported spontaneous precognitive dreams. After eight sleep laboratory nights with REM awakenings for dream collection, a word from the dream element list of Hall and Van de Castle’s (1966) book was chosen at random. An experimenter created a multi-sensory environment around this word, using items which were directed to visual, auditory, gustatory, olfactory and tactile-kinesthetic inputs to which the subject was exposed. Three independent judges rated each of the eight dream protocols against the eight words/descriptions of the multi-sensory experience. Five out of eight trials were rated correctly (p = .00018; Krippner et al., 1971). The second study with a slightly different design also yielded five hits (p = .0012; Krippner et al., 1972). Among the most impressive hit was the following dream account which was rated with an average agreement of 98.3 % by the three judges:

“Bob Morris does research on animal behavior and more specifically birds.... He’s been doing various research and studies with birds and he’s taken me out to see his sanctuary place where all the birds are kept.... I remember seeing various different kinds of doves. Ring-tailed doves, ordinary doves, Canadian geese...” (Krippner et al., 1972, p. 278, third dream report, post-sleep interview)

The subsequent waking experience consisted of a slide show with various pictures of birds selected at random.

Despite the fact that the above phenomena were studied in an artificial rather than a natural context, the two studies showed positive results. However, both studies used only a single subject and future research is needed therefore to expand these findings.

Influencing Factors

The occurrence of precognitive dreams correlates with dream recall frequency in general (Haraldsson, 1975; Palmer, 1979; Kohr, 1980; Thalbourne, 1984; 1994; Houran & Lange, 1998; Schredl, 1999b). This is expected, since a person who hardly recalls any dream will not be able to experience a precognitive dream. Equally plausible is the strong relationship between the reporting of precognitive dreams and a positive attitude towards parapsychological phenomena (e.g. Houran & Lange, 1998). The causality in this relationship, however, remains unclear. That is, persons interested in parapsychology may pay more attention to their dreams in order to detect links to subsequent events. Conversely, however, it may also be possible that a person who experienced an intense precognitive dream (maybe negatively toned) would develop an interest in parapsychology trying to understand the experienced phenomenon better.

Bender (1966) proposed that persons with ego-weakness (a psychoanalytic notion) are more likely to experience precognitive dreams and Schredl’s (1999b) finding that persons with thin boundaries reported precognitive dreams more often than persons with thick boundaries - even when dream recall frequency is statistically controlled - support and expand this notion. The boundary construct (Hartmann, 1991) is a broad concept; persons with thin boundaries are creative, empathic, vulnerable, have intense but stressful relationships, etc. This view is supported by Ross and Joshi’s (1992) finding of a positive correlation between the experience of parapsychological phenomena (including precognitive dreams) and the occurrence of dissociative experiences (e.g. depersonalisation, pseudo-hallucinations, psychogenic fugue). In addition, the reporting of paranormal experiences was related to sexual abuse during childhood (Ross & Joshi, 1992). Since severe traumata can cause dissociative disorders such as multiple personality disorder which is characterized by a confusion of mental boundaries, it may be hypothesized that traumata can make boundaries more permeable. Consistent with this hypothesis, Hearne (1984) found elevated scores of neuroticism in persons who responded to a newspaper announcement asking for precognitive dreams. Since Hearne’s sample was biased, i.e., persons responding to a newspaper announcement, this finding cannot be generalized. In a similar way, the above cited studies should be interpreted with caution since these studies utilized questionnaires to measure the occurrence or frequency of precognitive dreaming. However, as stated earlier, such questionnaires do not satisfy the criteria in Table 1. Therefore, future research applying more sophisticated measurement and inference techniques are needed to evaluate the previous research on personality and precognitive dreaming.

A largely unexplored field was recently investigated by Schredl (1999b). In two studies, several aspects of dreaming were related to the occurrence of precognitive dreams. The results indicated that persons with intense dreams and persons who reported that dreams affect their waking life (e.g. dreams which are helpful in solving problems, dreams affecting daytime mood, dreams stimulating creativity), also report more often precognitive dreams. Therefore, the experience of precognitive dreams seems to be part of a more general aspect of dream life which can be seen as a thin boundary between dreaming and subsequent waking life.

Personal Significance and Clinical Relevance

Stowell (1995) pointed out that while research in precognitive dreaming is focused on finding evidence for the existence of the phenomenon, studies investigating the effect of such dreams on the inner life of persons herself/himself are scarce. Case reports (Hastings, 1977; Sondow, 1988; Schredl, 1996; Stowell, 1997a, b) indicated that precognitive dreams can serve as preparation to the following event, e.g. the death of a close relative. In other words, the expression of emotions in a dream may facilitate the mourning process.

Halliday (1987) stressed the clinical relevance of precognitive dreaming since he observed that some persons suffer from precognitive dreams (his term is prophecy nightmares). Schredl (1996), for example, reported a case where the female dreamer experiences several dreams of muddy water and in the following few days a relative or close friend has died. This woman developed anxieties regarding her dreams because of their capacity to predict such negative events. Halliday (1987) suggested the use of insight-oriented therapeutic approaches as used also for ordinary dreams such as Gestalt techniques or the imagery rehearsal approach developed for the treatment of nightmares (Krakow & Neidhardt, 1992). Halliday (1987) further suggested directly testing the possibility of chance coincidence and addressing the possible superstition that dreams are seen as causes for subsequent events (sometimes found in young children).

The Present Research

The above review emphasizes the need to implement research designs and develop models for precognitive dreaming that have strong ecological validity for purposes of generalization, while maintaining a strict quantitative focus similar to experimental approaches. Moreover, any proposed model should account for the patterns of findings derived from studies of spontaneous cases and dream diaries. For the reasons outlined below, the approach adopted in the present research does not assume that experiences of precognitive dreaming are necessarily parapsychological in origin.

Contextual Variables. Despite the strict criteria given in Table 1 for identifying ostensibly genuine precognitive dreams, the fact remains that the contents of dreams are inherently ambiguous (Hobson, 1997) and that additional information is typically required to achieve a coherent interpretation of those contents. Research indicates that such additional information is frequently derived from the dreamer’s broadly defined “context,” which includes both state and trait factors (for an overview, see e.g., Houran, 1998). In this sense, the labeling of dream contents as “precognitive” is simply an interpretation of ambiguous dream stimuli. We have found that the interpretation of ambiguous stimuli is predictably guided by contextual variables such as the perceiver’s psychophysical state, embedded environmental cues, symbolic-metaphorical references, demand characteristics of the situation, and prior beliefs and expectations (Lange, Houran, Harte, & Havens, 1996; Houran & Lange, 1997; Lange & Houran, 1996; Houran, Lange, & Crist-Houran, 1997). Consistent with the findings by Krippner et al. (1971, 1972), it seems likely therefore that dreams are subject to the same influences as well (Houran, 1998).

Labeling. Belief in the paranormal strongly affects the recall and interpretation of ambiguous experience (Smith, 1992-93; Wiseman & Morris, 1995; Wiseman, Jeffreys, Smith, & Nyman, 1999). For example, laboratory experiments have confirmed that believers in the paranormal are less inclined than nonbelievers to consider coincidences as being the result of mere chance (Blackmore & Troscianko, 1985; Brugger, Landis & Regard, 1990; Blackmore, 1992), while believers are also more inclined to claim a relationship between coincidences and their own thoughts and actions (Brugger, Regard & Landis, 1991; Brugger, Regard, Landis, Cook, Krebs, & Niederberger, 1993). Moreover, the labeling of events and information can have a strong effect on people’s subsequent attitudes (Eiser, 1990) by making them resistant to change (Lange & Fishbein, 1983, Fishbein & Lange, 1990). Accordingly, we expect that once a non-chance interpretation of ambiguous events has been established, such interpretations continue to play an active role in believers’ cognitions.

Tolerance of Ambiguity. A series of studies (Lange & Houran, 1998, 1999b) indicated that an emotional and perceptual personality variable called “tolerance of ambiguity” plays an important role in the processing of ambiguous stimuli. Intolerance of ambiguity reflects the tendency to resort to black and white solutions characterized by premature closure, often at the neglect of consensual reality. In essence, an intolerance of ambiguity results in rapid and overconfident judgment of equivocal stimuli or events. As such, it is associated with perceiving ambiguous situations as threatening, whereas a tolerance of ambiguity is associated with perceiving ambiguous situations as desirable (Frenkel-Brunswick, 1949; Budner, 1962).

Consistent with this characterization, we (Lange & Houran, 1998, 1999b) have found that those with a high tolerance of ambiguity express little or no anxiety when presented with ambiguous stimuli. By contrast, individuals with a low tolerance of ambiguity often react with anxiety or fear. This aforementioned research also consistently identified tolerance of ambiguity as a correlate of belief in the paranormal. Houran and Williams (1998) subsequently discovered that tolerance of ambiguity was related only to specific types of paranormal beliefs and experiences, namely those that involve a reinterpretation of internal and physiological experience [e.g., beliefs suggesting the mind can expand beyond its usual boundaries, memories of reincarnation, visual apparitions, and vestibular alterations]. Among those paranormal beliefs and experiences associated with tolerance of ambiguity was precognitive dreaming (as measured by the question “There have been events that I dreamed about before the event occurred”). Path analyses reported by Houran and Lange (1998) extended this initial finding and established that precognitive dreaming was a byproduct of both belief in the paranormal and frequency of dream recall.

Nonlinearity. The various relations involving tolerance of ambiguity referred to above involve linear effects that were expressed exclusively in terms of standard bivariate correlation coefficients or regression weights. However, recent research (Lange & Houran, 2000) showed that tolerance of ambiguity has nonlinear effects in certain cases and that prediction is improved substantially by adopting a nonlinear approach as based on the mathematical theories by Thom (1975) pertaining to catastrophe models. Specifically, it was found that a cusp catastrophe significantly outperformed a standard linear regression model in predicting the formation of paranormal beliefs (R² = 0.954 vs. 0.305). Other studies (Houran & Lange, 1998; Lange & Houran, 2000) indicate that experiences of precognitive dreaming and the formation of paranormal beliefs share several important variables, and we propose therefore to study precognitive dreaming from a catastrophe perspective as well. In essence, catastrophe models describe how small changes in a systems independent variables can have large and discontinuous effects on a response (dependent) variable. Analogous to the sudden buckling of a beam under an increasing load, Lange and Houran’s (2000) results suggest that the labeling of a dream as precognitive occurs rather abruptly as more otherwise inexplicable explanations accumulate and are seized upon. As we discuss in greater detail in the following sections, the cusp model also explains why such changes are largely irreversible.

Starting with the work by Zeeman (1974), catastrophe models have a long history in the social sciences (Guastello, 1995). However, statistical problems have restricted their spread in the life sciences (Alexander, Herbert, DeShon, & Hanges, 1992; Oliva, Desarbo, Day, & Jedidi, 1987), and catastrophe models have not previously been used in research on precognitive dreams. For this reason, the following sections provide an introduction to these models as relevant to the present purposes as well as an overview of the statistical techniques needed for fitting catastrophe models. An elementary introduction to applied catastrophe theory can be found in Brown (1995), while Guastello (1995) provides a comprehensive review of the available psychological literature.

The Cusp Catastrophe

The most widely studied catastrophe model is the “cusp,” and it is this model that was used successfully in the study by Lange and Houran (2000). The cusp catastrophe is a three-dimensional curve whose first derivative is given by the equation:

(1)

Note that if, as in the present paper (see Method section), Z takes on only two possible values, then the variable Z can be rescaled such that Z³ = Z. In this case Equation 1 reduces to:

(2)

In Equations 1 and 2, Z represents the dependent variable, whereas X and Y represent two control variables. Because these two variables have quite different effects on Z, we first describe the pairwise relations between X and Z and between Y and Z.

Figure 1: The relation between the dependent variable (Z) and the asymmetry variable (X) while holding Y constant.

Figure 2: The relation between the dependent variable (Z) and the bifurcation variable (Y) while holding X constant.

As is shown in Figure 1, varying a cusp’s asymmetry (or “normal”) variable X for a fixed (but relatively high) level of Y produces a curve that resembles a cross-section of the pleat created when two opposite ends of a piece of fabric are pushed together. That is, the shape of a cross-section changes from approximately linear to an overlapping fold. In the folded portion, variations in X can cause dramatic effects since the value of Z may jump from the bottom plane to the top plane or vice-versa. Because the locations on the curve between these markers are inaccessible such jumps (up or down) occur at the markers only. Consequently, the Z values corresponding to the inaccessible region should not occur empirically (or, at least, they should occur infrequently), resulting in a bimodal distribution of Z. Although Z may show abrupt changes, its behavior is dampened by the fact that the system continues to adhere to the Z plane it currently occupies, unless it is “pushed too far” along the X-axis. As a result, the system exhibits hysteresis, i.e., a lag in behavior that acts as a form of memory.

Figure 2 shows the effects of variations in the bifurcation (or “splitting”) variable Y when X is held constant. Note that the change in Z has two characteristic features. First, as the value of Y moves away from the origin, a point is reached where the function bifurcates (i.e., Z takes one of two values). Second, once bifurcation has occurred, the magnitude of the differences between these two possible values increases with increasing Y. The preceding discussion indicated that the system does not arbitrarily jump between the two values of Y. Instead, all changes are completely determined by the preceding values of the X and Y variables, and the resulting dynamics can be studied in longitudinal research designs (Guastello, 1982; Lange, 1999; Lange, McDade and Oliva, 2000). However, longitudinal designs are not always feasible nor desirable and several applications have been reported in which the system of interest is observed only once (Guastello, 1995). In such instances, Z observations should form two layers, and -- due to the effects of hysteresis – one may find that two cases with identical X and Y control values exhibit different values for the dependent variable Z.

Figure 3: The Complete Three Dimensional Cusp Shape.

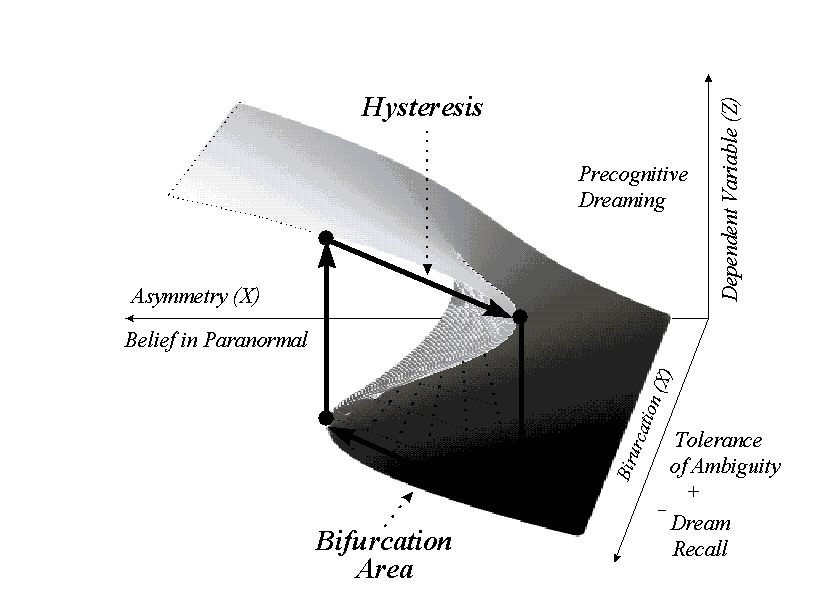
Figure 3 depicts the complete three-dimensional cusp that results when the effects of X and Y on Z are considered simultaneously. It can be seen that X and Y bear a nearly linear relation to Z for low values of the asymmetry variable X. In addition, the figure shows the existence of two different nearly linear (or, at least, continuous) planes for extreme values of X, regardless of the value of the bifurcation variable Y. However, these two variables produce highly discontinuous changes in Z for high values of Y combined with intermediate values of X. This particular combination of X and Y values constitutes the “bifurcation set” as indicated by the darkened area on the XY plane. As pointed out above, absent prior information concerning Z, the (X, Y) pairs in this set are associated with seemingly unpredictable and erratic changes in the dependent variable. We note that the cusp catastrophe derives its name from the characteristically peaked projection of the folded Z surface onto the XY plane. It is precisely this part of the cusp that is of greatest interest for the present purposes.

Hypotheses

It should be obvious that precognitive dreaming represents the variable Z in our cusp catastrophe formulation. The question arises however how belief in the paranormal, tolerance of ambiguity, and dream recall as identified by Houran and Lange (1998) should be mapped onto a cusp’s X and Y control variables. We advance the following hypotheses.

First, based on the findings by Lange and Houran (2000) we hypothesize that tolerance of ambiguity constitutes a bifurcation variable (Y) rather than an asymmetry variable. In particular, we expect that the interpretation of dreams as precognitive is likely to be avoided by those shunning non-standard explanations (which would be facilitated by intolerance of ambiguity). Second, in order to notice that one’s dreams might be related to subsequent waking experience, it is clearly necessary that such dreams be recalled in the first place. Thus, greater dream recall should increase the likelihood of noticing any correspondences, if only by chance. We hypothesize therefore that frequency of dream recall plays a role similar to tolerance of ambiguity, and it should therefore act as a bifurcation variable (Y). Finally, previous research strongly suggests that prior belief shapes the interpretation of ambiguous experiences, and not vice-versa (Lange & Houran, 1997; Lange & Houran, 1998, 1999b). Accordingly, we assume that the very interpretation of a dream as precognitive presupposes a belief in the paranormal, while the absence of such beliefs is a major factor in the rejection of dreams as precognitive. Thus, belief in the paranormal should contribute to the asymmetry variable (X) rather than the bifurcation variable. As a result, believers are expected to occupy the “high” plane of the cusp in Figure 3 whereas non-believers should be more likely occupy the “low” plane.

GEMCAT II

Analogous to the situation in structural modeling, our hypotheses imply that Y is a composite, or “latent,” variable that combines tolerance of ambiguity and dream recall as its indicator variables. Although latent variables pose no particular problem in linear modeling (see, e.g., Bollen, 1989), they greatly complicate the testing of specific hypotheses when dealing with (non-linear) catastrophe models (Brown, 1995; Cobb, 1981; Guastello, 1982), at least not without making strong additional assumptions (Alexander et al., 1992). However, Lange (1998) recently developed the GEMCAT II software that generalizes the model fitting approach pioneered by Oliva et al. (1987) while adding statistical tests of the model parameters. Extensive computer simulations reported in Lange, Oliva, and McDade (1999b) demonstrated the robustness of the GEMCAT II algorithm, even when very noisy indicator variables are used. This paper also introduced Pseudo-R² indices of fit, together with tests of statistical significance and competitive model testing.

Table 2: Definitions of the indicator variables and their operationalizations

Indicator variable	Description	Operationalization
x₁	Belief in the paranormal	Paranormal Belief subscale of AEI (Kumar et al., 1994)
y₁	Tolerance of ambiguity	Rasch version of MacDonald’s AT-20 (Lange & Houran, 1999a)
y₂	Dream Recall	Schredl et al (1997)
z₁	Precognitive dreaming	item # 29 on the AEI (Kumar et al., 1994)

In GEMCAT II, the variables X, Y, and Z may consist of arbitrary linear combinations of indicators variables, including fixed or variable offset values. Thus, in their most general form our hypotheses translate into the equations:

X = a₀ + a₁x₁, (3)

Y = b₀ + b₁y₁ + b₂y₂,

Z = g₀ + g₁z₁

where the symbols x₁, y₁, y₂, and z₁ denote the indicator variables listed Table 2. It is difficult to determine beforehand whether the offsets a₀, b₀, and g₀ are actually needed and empirical information is often needed to settle such questions (Brown, 1995). We further note that the algorithm requires that at least one of the Z indicator weights be fixed (Lange et al., 1999b; Oliva et al., 1987). Therefore, g₁ is set to 1.0 throughout this paper.

Each GEMCAT run provides a Pseudo-R² index of fit and an associated test of statistical significance (see, e.g., Bates & Watts, 1988). Such R² values are approximate only because they are derived by treating catastrophes as if they were linear models. It should be noted, however, that the Pseudo-R² index assumes continuous measures of X, Y, and Z. Since our measure of Z is two-valued (see Method) we expect that the Pseudo-R² obtained in the present research are inflated. To determine the statistical significance of the indicator weights GEMCAT II implements a bootstrap resampling approach (see, e.g., Efron & Tibshirani, 1993) which determines the statistical significance of the indicator weights by computing an Achieved Significance Level (ASL). Computing the ASL does not make any assumptions regarding the indicator weights’ sampling distributions and the resulting significance tests are distribution free. In addition, Lange et al. (1999c) describe how differences in fit for two or more models M₁, M₂, … (or two populations C₁, C₂, … ) can be tested by standard non-parametric tests (see, e.g., Marascuilo & McSweeney, 1977). Although this approach does not require that the models all be catastrophes, it does assume that they contain equal numbers of free parameters.

We point out that a different approach is required when M₁, M₂, … have unequal numbers of parameters and we refer the interested reader to the presentation in Lange et al. (1999c) for details.

An Overview

Since catastrophe theory has not previously been applied in precognitive dream research, we used Houran and Lange’s (1998) data set to refine the hypotheses summarized by Equation 3. The resulting formulation was then tested on a second, independent data set. Also, to establish more conclusively the validity of our basic hypotheses, we will consider two alternative formulations as well.

First, our hypotheses describe a cusp model in which belief in the paranormal functions as an asymmetry (X) variable, while tolerance of ambiguity and dream recall together play the role of the bifurcation variable (Y). In the remainder, we will refer to this model as Cusp₁. Although the finding of a high Pseudo-R² index is not inconsistent with Cusp₁, this alone would not exclude the possibility that paranormal belief is in fact a Y indicator or that tolerance of ambiguity and dream recall are really X indicators. Therefore, we will fit a second cusp model, Cusp₂, in which the roles of the X and Y indicator are reversed. That is, in Cusp₂ tolerance of ambiguity and dream recall are X indicators, whereas paranormal belief is a Y indicator. Our hypotheses entail that Cusp₁ should provide a better fit to the data than the alternative model Cusp₂ (Note 1).

Second, we pointed out earlier that Equations 1 and 2 are equivalent because Z represents a binary variable in the present research. Thus, if Y in Equation 1 takes on small values only, a (nearly) linear equation results (i.e., Z » X) that can be fitted by standard regression techniques. Although the finding of a superior fit of such a linear model does not really invalidate our hypotheses, it also provides very little reason to prefer the more complex cusp formulation over a simpler linear model. To address this issue, competitive model test will be performed between Cusp₁, Cusp₂, and a standard regression model which predicts precognitive dreaming as the weighted linear sum of tolerance of ambiguity, belief in the paranormal, and frequency of dream recall. That is:

z₁ = w₀ + w₁x₁ + w₂y₁ + w₃y₂ (4)

Study I

Method

Fifty undergraduate psychology students (27 women and 23 men, M _age = 25.8, SD_age = 8.5, range = 18-55 yrs.) completed the following questionnaires in random order. The symbols between parentheses refer to the row labels in Table 2.

Belief in the Anomalous/ Paranormal (x₁) was derived from the Anomalous Experience Inventory (AEI, Kumar, Pekala, & Gallagher, 1994). The reported reliability (KR-20 index) of this subscale is 0.77 (Gallagher, Kumar, & Pekala, 1994). Our measure of Precognitive Dreaming (z₁) is represented by the response (true/ false) to the statement “There have been events that I dreamed about before the event occurred,” which is contained in the Anomalous/ Paranormal Experience subscale of the AEI (derived from factor and cluster analyses). Responses of “true” were scored as 1, whereas responses of “false” were scored as 0. To maintain the “paranormal” context of the statement, it was left embedded in the AEI. Tolerance of Ambiguity (y₁) was measured using Lange and Houran’s (1999a) 18-item Rasch version of MacDonald’s (1970) AT-20 scale. The reported reliability of this interval-level scale is 0.68. Finally, we used an English language translation of Schredl’s frequency of dream recall questionnaire (see e.g., Schredl & Doll, 1997; Schredl, Jochum, & Sougoenet, 1997; Schredl & Montasser, 1996-1997) to measure Dream Recall (y₂). This measure reflects respondents’ answers to the question “How often have you recalled your dreams during the last few months?” with the following response options: “almost every morning,” “several times a week,” “about once a week,” “two or three times a month,” “about once a month,” “less than once a month,” or “never.” These responses were scaled as 6, 5, 4, 3, 2, 1, and 0, respectively.

Results

Preliminaries. A series of preliminary GEMCAT II runs indicated that offsets b₀ and g₀ in Equation 3 were superfluous and they were therefore omitted (Note 2). Consequently, our main hypothesis is represented by Cusp₁ as is shown below:

Cusp₁:

X = a₀ + a₁x₁, (5)

Y = b₁y₁ + b₂y₂,

Z = g₁z₁

To test whether the assignment of the indicator variables to either X or Y is correct (see Table 2), we define a model Cusp₂ in which the X and Y indicator variables are swapped relative to Equation 5 while keeping the X offset. In other words:

Cusp₂:

X = b₀ + b₁' y₁ + b₂' y₂, (6)

Y = a₁' x₁,

Z = g₁z₁

While g₁ has the value 1 in Equation 5 as well as 6, the values of the a’ and b’ in Equation 6 almost certainly differ from the corresponding a and b weights in Equation 5. However, the definitions of the indicators x₁, y₁, y₂, and z₁ remain unchanged, i.e., they continue to correspond to the definitions given in Table 1.

Table 3: The indicator weights’ plugin values and model fit of the linear model and the cusp catastrophe model in Study I (N = 50).

					Paranormal			Tolerance of			Dream			Precognitive		(Pseudo-)			(Pseudo-)
		Constant			Belief			Ambiguity			Recall			Dreaming		R²	df₁	df₂	F
Linear (Eq. 4)	W^a	-0.778	*^b	W	0.059	*	W	0.027	*	W	0.047		Z	1.000	^c	0.320	3	46	7.221	***

Cusp₂ (Eq. 6)	X	-0.556		Y	0.097		X	0.033		X	0.055		Z	1.000		0.334	3	46	7.672	***^d

Cusp₁ (Eq. 5)	X	0.041	*	X	-0.011	*	Y	0.024	***	Y	0.067	***	Z	1.000		0.949	3	46	282.793	***^d
SE₁		0.052			0.052			0.004			0.020			---

* p < .05 ** p < .01 *** p < .001 (applies also to ASL levels)

a) Each indicator weight is prefixed by the (latent) variable to which it contributes (see Equations 4, 5, and 6)

b) The significance levels for the linear model weights derives from standard t-tests, while those for Cusp₁ and Cusp₂ reflect ASL values derived from 500 bootstrap replications

c) This weight was fixed at the value 1 for reasons described in the text.

d) Pseudo values (see text)

Table 4: Pairwise comparisons of the fit of Cusp₁, Cusp₂, and the linear model in Study I (N = 50).

Cusp₁	5.333*
Cusp₂	-0.246	-5.633*
	Linear	Cusp₁

* p < 0.001

Note: Shown are the normal deviates (z-values) produced by Wilcoxon’s Signed Rank test. A positive entry indicates that the model identified by the row label is better than that identified by the column label.

Model Identification. Table 3 (left side of table) shows the parameters of the Linear model (Eq. 4), Cusp₁ (Eq. 5) and Cusp₂ (Eq. 6) as well as their R² type indices of fit (right side of table). As expected, Cusp₁ (Pseudo-R² = 0.949) shows a better fit to the data than either the Linear model (R² = 0.320) or the alternative cusp formulation, Cusp₂ (Pseudo-R² = 0.334). As pointed out earlier, the Pseudo-R² values may be inflated due to the binary nature of Z, and the three models were therefore also compared via non-parametric tests. Consistent with the obtained order of the (Pseudo-) R² values, the results of Kendall’s W test over these three models’ squared residuals indicates that their fit differs significantly (W = 0.395, c²₂ = 39.250, p < 0.001). As is shown in Table 4, subsequent pairwise comparisons between the three models indicate that Cusp₁ performs significantly better than other two models (p < .001), while Cusp₂ and the linear model show a similar performance (p > .20). Thus, Cusp₂ and the linear model can both be rejected, while the proposed assignment of the indicator variables to the latent variables X and Y in Cusp₁ is justified. For these reasons, the remainder of this section deals exclusively with the best fitting model, Cusp₁.

Figure 4: Actual vs. Predicted in Study I (Z by Y)

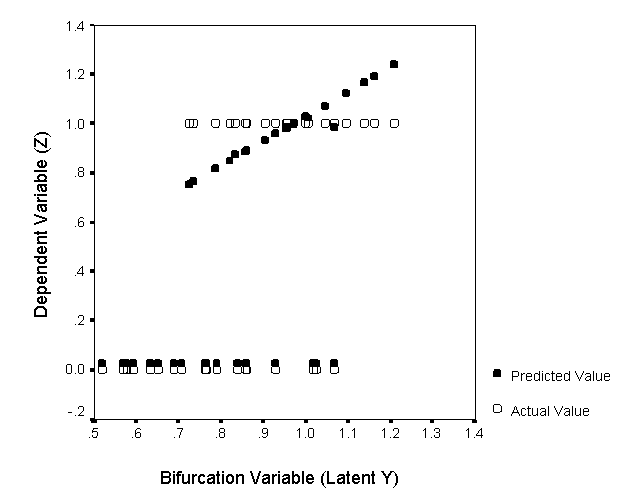
As predicted, Table 3 shows that Tolerance of Ambiguity (b₁ = 0.024, ASL < 0.001) and Dream Recall (b₂ = 0.067, ASL < 0.001) both contribute positively to the latent bifurcation variable Y in Cusp₁. That is, as is shown in Y by Z cross-section in Figure 4, greater Tolerance of Ambiguity and greater Dream Recall increase the magnitude of the bifurcation in Precognitive Dreaming. Analogous to the theoretical situation depicted in Figure 1, the observed values of Z in Figure 4 diverge with increasing Y, thereby producing the expected bimodal distribution of Z. Note that our data only occupy the rightmost part of Figure 2 as the Z values do not meet for the lowest values of Y. Table 3 further shows that Paranormal Belief contributes significantly negative to the latent variable X (a₁ = -0.011, ASL < 0.05) while the value of the X offset is statistically significant (a₀ = 0.041, ASL < 0.05).

Study II

The first study involved several decisions and refinements of Cusp₁ that were contingent on properties of the particular sample being used. Therefore, we replicated Study I using a new sample of respondents consisting of 59 undergraduate psychology students (28 women and 31 men, M _age = 24.5, SD_age = 8.6, range = 18-59 yrs.). The same questionnaires were administered and identical procedures were followed as in Study I.

Table 5: The indicator weights’ plugin values and model fit of the linear model and the cusp catastrophe model in Study II (N = 59).

					Paranormal			Tolerance of			Dream			Precognitive	(Pseudo-)			(Pseudo-)
		Constant			Belief			Ambiguity			Recall			Dreaming ^c	R²	df₁	df₂	F
Linear (Eq. 4)	W^a	0.046	*^b	W	0.029	*	W	0.002	*	W	0.078		Z	1.000	0.102	3	55	2.077

Cusp₂ (Eq. 6)	X	0.650		Y	0.094		X	-0.020		X	-0.002		Z	1.000	0.780	3	52	64.950	***^d

Cusp₁ (Eq. 5)	X	0.157	*	X	-0.018	*	Y	0.029	***	Y	0.053	***	Z	1.000	0.959	3	55	426.813	***^d
SE₁		0.037			0.004			0.004			0.021			---
t(107) ^e		-1.811	^f		0.137			-0.917			0.476			---

* p < .05 ** p < .01 *** p < .001 (applies also to ASL values)

a) Each indicator weight is prefixed by the (latent) variable to which it contributes (see Equations 4, 5, and 6)

b) The significance levels for the linear model weights derives from standard t-tests, while those for Cusp₁ and Cusp₂ reflect ASL values derived from 500 bootstrap replications

c) This weight was fixed at the value 1 for reasons described in the text.

d) Pseudo values (see text)

e) The t value was computed based on the standard error , where the subscripts I and I refer to quantities pertaining to Studies I and II, respectively.

f) p < .10 (2-sided)

Table 6: Pairwise comparisons of the fit of Cusp₁, Cusp₂, and the linear model in Study II (N = 59).

Cusp₁	6.514*
Cusp₂	5.510*	-4.544*
	Linear	Cusp₁

* p < 0.001

Figure 5: Actual vs Predicted Study II (Z by Y)

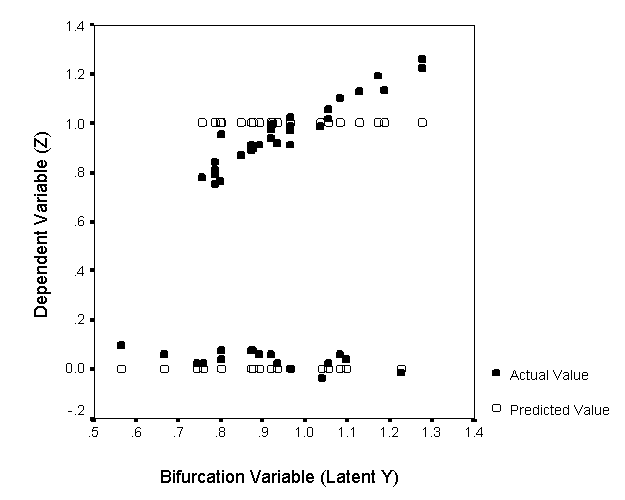
Results

The results of Study II are highly similar to those obtained earlier.

First, as is shown in Table 5, Cusp₁ again provided the best fit to the data (Pseudo-R² = 0.959), followed by Cusp₂ (Pseudo-R² = 0.780) and the linear model (R² = 0.102). Consistent with the large differences among the (Pseudo-) R² values, the difference in fit among the three models is highly significant (W = 0.546, c²₂ = 64.373, p < 0.001), while Table 5 shows that Cusp₁ again fits significantly better than both Cusp₂ and the linear model (p < 0.001). However, in contrast to Study I, Cusp₂ now performs significantly better than the linear model (p < 0.001). Third, inspection of Tables 3 and 5 reveals that the indicator weights for Cusp₁ are highly similar to those in Studies I. To obtain a formal test of this observation we performed t-tests for independent samples over the four free indicator weights for Cusp₁ in the two studies. As is described in Footnote e of Table 5, this test is based on the standard errors of the indicator weights (SE₁) as produced by GEMCAT II’s bootstrap procedure. The t-values in the bottom row of Table 5 indicate that all four tests fail to reach statistical significance (all p > 0.05, 2-sided). Finally, note that the Y by Z cross-section shown in Figure 5 strongly resembles its counterpart in Study I.

Ancillary Analyses

General. Analysis of the combined data of Studies I and II (N = 109) yielded results that generally agree with past findings related to the frequency of precognitive dreaming. However, while a greater proportion of women (0.66) reported precognitive dreams than men (0.59), this difference fails to reach statistical significance (p = .301 by Fishers’ exact test). Likewise, the mean age of those reporting precognitive dreams was less (M = 24.29 yrs.) than that of those not reporting such dreams (M = 26.49 yrs.). Again, however, the difference was not statistically significant (t(107) = 1.30, p > .19). Finally, as might be expected, dream frequency was significantly greater (t(107) = -3.06, p < .01) for self-reported precognitive dreamers (M = 4.60) than for non-precognitive dreamers (M = 3.76).

Gender. To further explore the effect of gender, we created one data set containing only men (N = 51) and another containing only women (N = 58) by combining all available cases of Studies I and II. Next, Cusp₁ was fitted to each data set. Table 7 reveals that men show a slightly better fit (R² = 0.967) than women (R² = 0.941) and a Mann-Whitney U test over the residuals indicated that this difference in fit is statistically significant (z = -2.181, p < 0.05). Also, the box plots in Figure 6 show that men’s residuals have more outliers and a slightly smaller standard deviation (SD = 0.090) than those for the women (SD = 0.116). However, men’s and women’s indicator weights all have the same signs and they are of comparable magnitudes. Further, all pairwise comparisons of these weights by gender failed to reach statistical significance as indicated by the values of the t statistics shown in the bottom row of Table 6 (all p > 0.10). Finally, the YZ cross-sections shown in Figures 7 and 8 show highly similar patterns of actual vs. predicted values for men and women. We conclude therefore that Cusp₁ applies about equally well to both sexes.

Table 7: The indicator weights’ plugin values and model fit of Cusp₁ for men (N = 51) and women (N = 58) as estimated based on the combined data sets of Studies I and II.

						Indicator Variables							Fit Statistics
			Latent X				Latent Y			Z
						Tolerance of		Dream		Precognitive	Pseudo-			Pseudo-
Gender	Model	Constant		Belief		Ambiguity		Recall		Dreaming ^b	R²	df₁	df₂	F
Men	Cusp	0.099	*** ^a	-0.012	**	0.026	***	0.066	*	1.000	0.967	3	47	460.678	***
	SE_Cusp	0.034		0.004		0.003		0.017
Women	Cusp	0.169	***	-0.018	**	0.030	***	0.045	*	1.000	0.941	3	54	287.954	***
	SE_Cusp	0.046		0.006		0.005		0.025
Men vs. Women	t(105) ^c	-1.227	^d	0.850		-0.693		0.697

* p < .05 ** p < .01 *** p < .001 (including ASL values)

a) The significance levels of each indicator weight as estimated by the ASL over B = 500 bootstrap replications.

b) The weight of this indicator was fixed at the value 1 for reasons described in the text.

c) Computed using the error for each pair of free indicator weights.

d) p > 0.10 (2-sided)

Figure 6: Boxplot of Residuals by Gender (Study I + II).

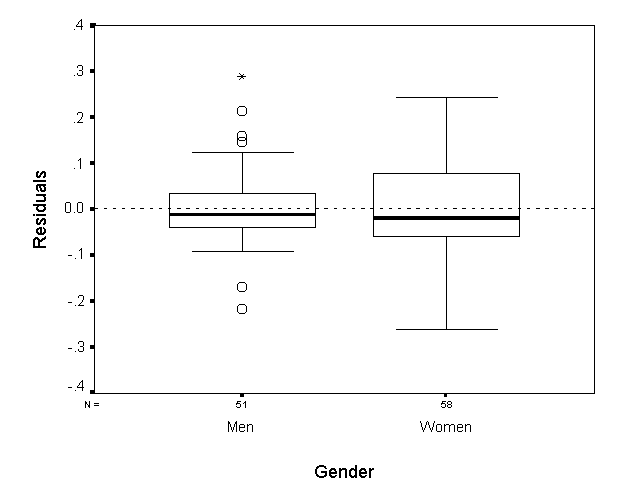
Figure 7: Z by Y for Men (Study I + II, N = 51)

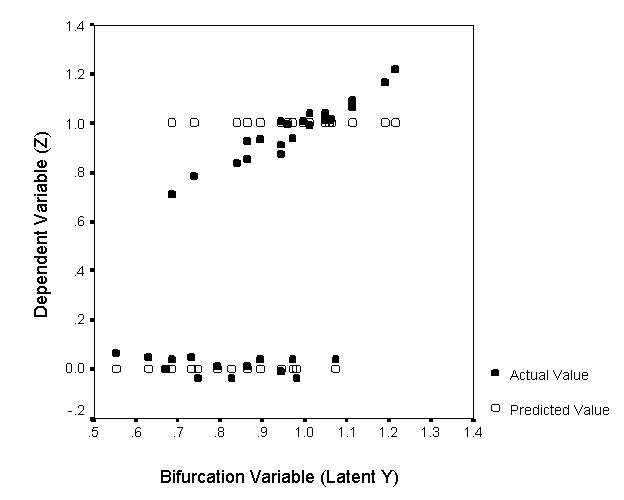
Figure 8: Z by Y for Women (Study I + II, N = 58).

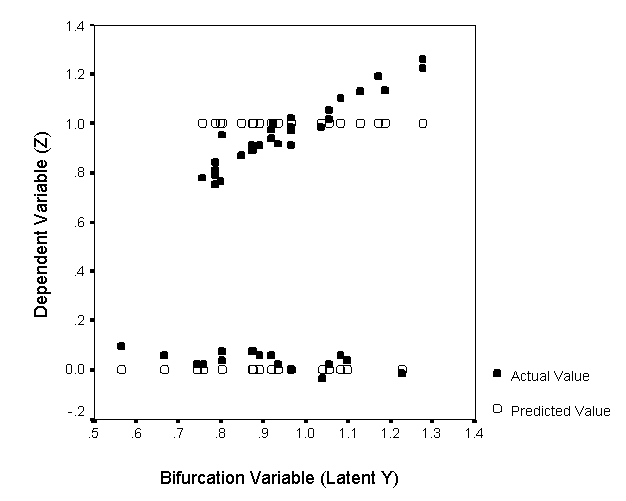
Linear Models vs the Cusp. To highlight the differences between a linear model of precognitive dreaming and a cusp formulation we consider Equation 2 in more detail. In particular, since our measure of Precognitive Dreaming is binary (i.e., Z = 0 or Z = 1), it is instructive to consider the behavior of Cusp₁ for these two possible values.

First, note that substitution of Z = 0 (indicating the absence of Precognitive Dreaming) into Equation 2 yields 0 - X - 0.Y = 0, which simplifies to (Note 3):

X = 0. (7)

The most important feature of this equation is that it does not contain the variable Y, i.e., the values of Tolerance of Ambiguity and Dream Recall are irrelevant while Paranormal Belief is the only variable responsible for keeping Z = 0. As such, Equation 7 strongly supports the conclusions reached in previous research (Lange & Houran, 1997; Lange & Houran, 1998; Lange & Houran, 1999b) that belief is the single most important factor in the interpretation of ambiguous stimuli as “paranormal.”

Second, substitution of Z = 1 (indicating the occurrence of Precognitive Dreaming) into Equation 2 yields 1 - X - 1.Y = 0, or:

Y = 1 - X. (8)

In other words, the occurrence of Precognitive Dreaming presupposes a negative correlation between the latent variables X and Y and the data support this conclusion since r_XY = -.488 (p < .001) for Z = 1. Note that we saw earlier that Paranormal Belief contributed significantly negative to X, and thus the sign of this variable is actually positive in Equation 8. As a result, Tolerance of Ambiguity, Dream Recall, and Paranormal Belief variables all contribute positively to Precognitive Dreaming.

Figure 9: A comparison of the linear model and Cusp₁ using all available data points (Study I + II, N = 109).

Taken together, Equations 7 and 8 imply that the functionality of the various indicator variables changes depending on the value of the variable Z. Figure 9 contrasts this behavior with that of the linear model by plotting the predicted values of the linear model and those for Cusp₁ against the latent bifurcation variable Y using all available cases (N = 109). This figure illustrates that the changes in the predictions produced by the linear model can only be proportional to changes in the predictor variables, while for each value of the predictor variable Y there is only one prediction Z. However, since Z is bimodal, many of the predictions produced by the linear model simply do not correspond to the data. As a result, the overall fit is poor. For instance, the R² fit of the linear model over all 109 cases is only 0.178.

By contrast, cusp catastrophes divide their predictor variables into two types (X and Y). Variations in X values allows an appropriate cusp to produce different predictions for the same value of Y (hysteresis), thereby avoiding generating non-occurring data values. It is precisely for this reason that Cusp₁ yielded a superior fit relative to the linear model.

Summary and Discussion

As anticipated, the nonlinear models showed a significant improvement in fit over a competing linear model in both experiments. In other words, the findings strongly support the basic hypothesis that precognitive dreaming is better described by a cusp catastrophe than by the linear models such as used in Houran and Lange (1998). However, the cusp formulation proved successful at a more detailed level as well. For instance, tolerance of ambiguity and dream recall loaded significantly on the latent Y variable. Thus, as hypothesized, these variables govern the cusp’s bifurcation behavior that corresponds to the binary measure of precognitive dreaming. Next, belief in the paranormal functioned as an asymmetry variable (X). Since variables of this type govern the overall level of the cusp response surface, we conclude that paranormal beliefs mainly serve to support the interpretation of otherwise ambiguous dream contents as precognitive. Further, the preceding interpretation is supported by the finding that an alternative cusp formulation in which the roles of the X and Y indicators are reversed provided a significantly poorer fit to the data in both experiments. Also, additional analyses showed that gender did not play a substantial role in the model fit, thereby increasing the generality of the cusp formulation. Finally, although the cusps’ Pseudo-R² values of fit are possibly inflated due to the binary nature of the dependent variable Z, we note that the relative magnitudes of these statistics agree with the order implied by the results of standard non-parametric tests over the models’ squared residuals.

These results are consistent with the hypothesis that some experiences of precognitive dreams are illusions, i.e., coincidences between the contents of dreaming and waking experience that are noticed due to frequency of dream recall and given credence due to the combined effects of belief in the paranormal and a tolerance of ambiguity. Although this proposal is not new, we believe that ours is the first empirically-derived, process model that explains the specific psychological mechanisms behind these experiences. Further, our nonlinear model accounts for the general relationship between dream recall and the experience of extrasensory perception (Haraldsson, 1975; Palmer, 1979; Kohr, 1980; Thalbourne, 1984; 1994; Houran & Lange, 1998; Schredl, 1999b), and it explains the exponential decline effect associated with precognitive dreaming (Green, 1960; Orme, 1974; Sondow, 1988; de Pablos, 1998) as an artifact of memory, i.e., less “hits” are reported over time because ambiguous dream contents are gradually forgotten and this prevents the percipient from finding correspondences with waking experience. Moreover, aside from reporting or researchers’ bias, it is understandable why negative themes and strong emotional responses may be predominant in experiences of precognitive dreams. Vivid and intense dream content often induces strong emotional reactions in the dreamer, and consequently these types of dreams are more easily remembered than dreams with mundane content. Our model does not directly address the findings of the Maimonides parapsychological dream studies, which arguably had more to do with apparent telepathy (cf. Bem & Honorton, 1994) than precognitive dreaming. Still, our results have implications for enhancing the methodologies of laboratory studies of precognitive dreaming. Our model suggests that experiences of precognitive dreaming occur because the contents of both waking and dream experience are largely ambiguous and therefore susceptible to numerous interpretations or selective reconstruction. Further, it appears that the types of information most likely to be experienced as “precognitive” involve situations that correspond to normal waking experience (we stress that crises and other negative or fluke events are also part of a continuum of normal waking experience). Therefore, we suggest that the second criterion in Table 1 (i.e., a “dream must include enough details to render chance fulfillment unlikely”) should be more stringent. Specifically, targets for laboratory studies should be as unambiguous as possible while simultaneously being of a variety that does not easily correspond to normal waking experience. We anticipate that applying these precautions in laboratory studies will safeguard against chance hits due to the variance in the randomization and judging procedures.

While the proposed cusp model explains some forms of precognitive dreaming (or perhaps the general tendency to notice chance correspondences between dreaming and waking experience), it is not clear whether it applies to cases that satisfy all the criteria listed earlier in Table 1. For instance, we did not differentiate between the exact contents of the dreams, nor did we take into account the effect these dreams had on the participants. Such factors are likely to be relevant since Stowell’s (1997a, b) phenomenological study indicated that at least four different types of precognitive dreams can be distinguished. A first type provides information about non-traumatic situations; a second type brings guidance to the dreamer; another relates negative situations about which it is impossible to take action; a final type provides information about situations where intervention is possible. Thus, we propose that future research might profitably investigate whether our model applies differentially to the four types of precognitive dreams as distinguished by Stowell (1997a, b). In addition, some methodological improvements are needed. We suggest that our dichotomous measure of precognitive dreaming be replaced with a measure of the frequency of precognitive dreaming that better conforms to the criteria in Table 1. For example, we are planning a replication study in which a frequency of dream recall measure is administered to a sample of self-described “psychics” who claim to have recurrent precognitive dreams that meet the explicit criteria in Table 1. Further, because only one of our indicator variables (i.e., the Rasch version of the AT-20, Lange and Houran, 1999a) is guaranteed to yield data at an interval level of measurement, the present results may depend partly on the particular operationalizations of the indicator variables. Further, in light of previous findings indicating age and gender effects in precognitive dreaming, we propose that any biasing effects in all indicator variables should be eliminated using the “purification” methods outlined in Lange, Irwin and Houran (2000; cf. Lange, Thalbourne, Houran, & Storm, in press).

On a more general level, we have again found that some types of perceived paranormal experiences are best modeled as a process of misattribution. This finding agrees with those who suggest that paranormal beliefs and experiences are misinterpretations of normal events (see Irwin, 1999, p 280). Yet, paranormal beliefs and experiences should not be regarded as a pathological or abnormal behavioral phenomenon. Rather, such beliefs and experiences can serve adaptive functions. For instance, Irwin (1999) noted that “By incorporating a system of paranormal beliefs, the individual has a cognitive framework for effectively structuring many events and experiences in life so that they appear comprehensible and thereby able to be mastered, at least intellectually” (p. 291). Accordingly, we hypothesize that some experiences of precognitive dreaming are not paranormal glimpses of the future but rather are the normal byproducts of people’s attempts to understand ambiguous stimuli in the present. The fact that the type of “precognitive dream” described by item # 29 on the Anomalous Experiences Inventory can largely be reduced to the dynamic interactions of three main variables (i.e., belief in the paranormal, dream recall, and tolerance of ambiguity) bolsters this conclusion. Of course, only time will tell if our hypothesis is correct.

Reference Notes

1) It is generally advisable that a simpler catastrophe model, the Fold, should be tested first (Lange & Houran, 2000). However, this consideration does not apply in the present case because the dependent variable Z (Precognitive Dreaming) is operationalized by a binary measure (see Method section). In this case, the fit of a Fold catastrophe is identical to that of a linear model with the same predictor variables.

2) The version of GEMCAT II used in the present research (V 1.3) is the result of a progressive series of enhancements of this program (Lange, 1998; Lange et., 1999a, b) and it is anticipated that a newer version will become available later. A copy of the latest GEMCAT II, together with instructions for its use, can be downloaded from the internet web site: <http://www.sbm.temple.edu/~oliva/cat-theory.htm>.

3) Although Equation 7 is true when Equation 2 fits perfectly, the actual value of X depends on the extent to which GEMCAT II is able to minimize the residual error (e) in the probabilistic version of Equation 1, i.e., (Z³ - X - ZY)² = X² = e². In support of our contentions, X² and e² are identical for Z = 0 (M = .002, SD = .0019, r = 1.000). By contrast, the median values of X² and e² differ almost by a factor 10 (Md_X2 =8.279E-04, Md_e2 = 7.452E-03, z = -5.286, p < .001) for Z = 1 as indicated by a Wilcoxon’s Signed Rank Test while their correlation (r = -.161, p > .18) fails to reach statistical significance.

References

Alexander, R., Herbert, G., DeShon, R., & Hanges, P. (1992). An examination of least-squares regression modeling of catastrophe theory. Psychological Bulletin, 111, 366-374.

Barker, J. C. (1967). Premonitions of the Aberfan disaster. Journal of the Society for Psychical Research, 44, 169-181.

Bates, D. M., & Watts, D. G. (1988). Nonlinear regression analysis and its applications. New York: Wiley & Sons.

Bem, D. J., & Honorton, C. (1994). Does psi exist? Replicable evidence for an anomalous process of information transfer. Psychological Bulletin, 115, 4-18.

Bender, H. (1966). The Gotenhafen case of correspondence between dreams and future events: A study of motivation. International Journal of Neuropsychiatry, 2, 398-407.

Besterman, T. (1933). Report of inquiry into precognitive dreams. Proceedings of the Society for Psychical Research, 41, 186-204.

Blackmore, S. (1992). Psychic experiences: Psychic illusions. Skeptical Inquirer, 16, 367-376.

Blackmore, S., & Troscianko, T. (1985). Belief in the paranormal: Probability judgments, illusory control, and the “chance baseline shift.” British Journal of Psychology, 76, 459-468.

Bollen, K. A. (1989). Structural equations with latent variables. New York: Wiley.

Botman, H. I., & Crovitz, H. F. (1989-90). Dream reports and autobiographical memory. Imagination, Cognition and Personality, 9, 213-224.

Brown, C. (1995). Chaos and catastrophe theories. Thousand Oaks, CA: Sage.

Brugger, P., Landis, T., & Regard, M. A. (1990). A ‘sheep-goat effect’ in repetition avoidance: Extra-sensory perception as an effect of subjective probability? British Journal of Psychology, 76, 459-468.

Brugger, P., Regard, M. A., & Landis, T. (1991). Belief in the paranormal and illusory control: A replication. Journal of Psychology, 125, 501-502.

Brugger, P., Regard, M. A., Landis, T., Cook, N., Krebs, D., & Niederberger, J. (1993). ‘Meaningful’ patterns in visual noise: Effects of lateral stimulation and the observer’s belief in ESP. Psychopathology, 26, 261-265.

Budner, S. (1962). Intolerance of ambiguity as a personality variable. Journal of Personality, 30, 29-50.Clericus, J. (1918). Zum Wahrtraum des Bischofs Lanyi von Großwardein. Psychische Studien, 45, 465-468.

Cobb, L. (1981). Parameter estimation of the cusp catastrophe model. Behavioral Science, 23, 75-78.

De Pablos, F. (1998). Spontaneous precognition during dreams: Analysis of a one-year naturalistic study. Journal of the Society for Psychical Research, 62, 423-433.

Dunne, J. W. (1927). An experiment with time. New York: Macmillan.

Efron, B., & Tibshirani, R. J. (1993). An introduction to the bootstrap. New York: Chapman & Hall.

Eiser, J. R. (1990). Social judgment. Pacific Grove, CA: Brooks/Cole.

Emery, M. (1991). Programming the precognitive dream. Association for the Study of Dreams Newletter, 8, 7-15.

Fishbein, M., & Lange, R. (1990). The effects of crossing the midpoint on belief change: A replication and extension. Personality and Social Psychology Bulletin, 16,189-199.

Frenkel-Brunswik, E. (1949). Intolerance of ambiguity as an emotional and perceptual personality variable. Journal of Personality, 18, 108-143.

Gallagher, C., Kumar, V. K., & Pekala, R. J. (1994). The anomalous experiences inventory: Reliability and validity. Journal of Parapsychology, 58, 402-428.

Green, C. (1960). Analysis of spontaneous cases. Proceedings of the Society for Psychical Research, 53, 97-161.

Guastello, S. (1982). Moderator regression and the cusp catastrophe: Application to two-stage personnel selection, training, therapy, and policy evaluation. Behavioral Science, 27, 259-272.

Guastello, S. J. (1995). Chaos, catastrophe, and human affairs. Mahwah, New Jersey: Lawrence Erlbaum.

Hall, C. S., & Van de Castle, R. L. (1966). The content analysis of dreams. New York: Appleton-Century-Crofts.

Halliday, G. (1987). Therapy for prophecy nightmares. Journal of Contemporary Psychotherapy, 17, 217-224.

Haraldsson, E. (1975). Reported dream recall, precognitive dreams, and ESP. In Research in parapsychology 1974. Metuchen: Scarecrow Press.

Haraldsson, E. (1985). Representative national surveys of psychic phenomena. Journal of the Society for Psychical Research, 53, 145-158.

Harley, T. A. (1989). PSI missing in a dream clairvoyant experiment. Journal of the Society for Psychical Research, 56, 1-7.

Hartmann, E. (1991). Boundaries in the mind. New York: Basic Books.

Hastings, A. C. (1977). Dreams of future events: Precognitions and perspectives. Journal of the American Society of Psychosomatic Dentistry and Medicine, 24, 51-60.

Hearne, K. M. T. (1984). A survey of reported premonitions and of those who have them. Journal of the Society for Psychical Research, 52, 261-270.

Hearne, K. M. T. (1986). An analysis of premonitions deposited over one year from an apparently gifted subject. Journal of the Society for Psychical Research, 53, 376-382.

Hendricks, L. L. (1989). Discovering my biblical dream heritage. San Jose: Resource.

Hobson, J. A. (1997). Dreaming as delirium: A mental status analysis of our nightly madness. Seminars in Neurology, 17, 121-128.

Houran, J. (1998). Complement to “Ratio of male and female characters in a dream series.” Perceptual and Motor Skills, 86, 1469-1470.

Houran, J., & Lange, R. (1997). Hallucinations that comfort: Contextual mediation of deathbed visions. Perceptual and Motor Skills, 84, 1491-1504.

Houran, J., & Lange, R. (1998). Modeling precognitive dreams as meaningful coincidences. Perceptual and Motor Skills, 83, 1411-1414.

Houran, J., Lange, R., & Crist-Houran, M. (1997). An assessment of contextual mediation in trance states of shamanic journeys. Perceptual and Motor Skills, 85, 59-65.

Houran, J., & Williams, C. (1998). Relation of tolerance of ambiguity to global and specific paranormal experience. Psychological Reports, 83, 807-818.

Irwin, H. J. (1999). An introduction to parapsychology (3^rd ed.). Jefferson, NC: McFarland.

Jackson, M. P. (1967). Suggestions for a controlled experiment to test precognition in dreams. Journal of the American Society for Psychical Research, 61, 346-353.

Kohr, R. L. (1980). A survey of PSI experiences among members of a special population. Journal of the Amercian Society for Psychical Research, 74, 395-411.

Krakow, B., & Neidhardt, J. (1992). Conquering bad dreams and nightmares: A guide to understanding, interpretation and cure. New York: Berkeley.

Krippner, S., Honorton, C., & Ullman, M. (1972). A second precognitive dream study with Malcolm Bessent. Journal of the American Society for Psychical Research, 66, 269-279.

Krippner, S., Ullman, M., & Honorton, C. (1971). A precognitive dream study with a single subject. Journal of the American Society for Psychical Research, 65, 192-203.

Kumar, V. K., Pekala, R. J., & Gallagher, C. (1994). The Anomalous Experiences Inventory. Unpublished Psychological Test. West Chester, PA: West Chester University.

Lange, R. (1998, July 28 - August 1). GEMCAT II : A distribution-free method for testing the statistical properties of Thom's catastrophe equations as defined by sets of arbitrary latent variables. Paper presented at the Eighth Annual Conference of the Society for Chaos Theory in Psychology and the Life Sciences, Boston, MA.

Lange, R. (1999). A cusp catastrophe approach to the prediction of temporal patterns in the kill dates of individual serial murderers. Nonlinear Dynamics, Psychology, & Life Sciences, 3, 143-159.

Lange, R., & Fishbein, M. (1983). The effects of category differences on belief change and agreement with the source of persuasive communication. Journal of Personality and Social Psychology, 44, 933-941.

Lange, R., & Houran, J. (1996). Role of contextual mediation in direct versus reconstructed angelic encounters. Perceptual and Motor Skills, 83, 1259-1270.

Lange, R., & Houran, J. (1997). Death anxiety and the paranormal: The primacy of belief over experience. Journal of Nervous and Mental Disease, 185, 584-586.

Lange, R., & Houran, J. (1998). Delusions of the paranormal: A haunting question of perception. Journal of Nervous and Mental Disease, 186, 637-645.

Lange, R., & Houran, J. (1999a). Scaling MacDonald's AT-20 using item-response theory. Personality and Individual Differences, 26, 467-475.

Lange, R., & Houran, J. (1999b). The role of fear in delusions of the paranormal. Journal of Nervous and Mental Disease, 187, 159-166.

Lange, R., & Houran, J. (2000). Modeling Maher’s attribution theory of delusions as a cusp catastrophe. Nonlinear Dynamics, Psychology, and Life Sciences, 4, 235-254..

Lange, R., Houran, J., Harte, T. M., & Havens, R. A. (1996). Contextual mediation of perceptions in hauntings and poltergeist-like experiences. Perceptual and Motor Skills, 82, 755-762.

Lange, R., Irwin, H. J., & Houran, J. (2000). Top-down purification of Tobacyk's Revised Paranormal Belief Scale. Personality and Individual Differences, 29, 131-156.

Lange, R., Oliva, T., & McDade, S. (1999a, June 13-16). Multivariate catastrophe modeling with GEMCAT II as applied to organizational product adoption. Paper presented at the AMA ART Forum, Sante Fe, NM.

Lange. R., McDade, S., and Oliva, T.A.(2000). A catastrophe model of organizational product adoption. Manuscript submitted for publication.

Lange, R., Oliva, T. A., & McDade, S. R. (1999b). An algorithm for estimating multivariate catastrophe models: GEMCAT II. Manuscript submitted for publication.

Lange, R., Thalbourne, M. A., Houran, J., & Storm, L. (in press). The Revised Transliminality Scale: Reliability and validity data from a Rasch top-down purification procedure. Consciousness and Cognition.

MacDonald, J., A.P. (1970). Revised scale for ambiguity tolerance: Reliability and validity. Psychological Reports, 26, 791-798.

Marascuilo, L. A., & McSweeney, M. (1977). Nonparametric and distribution-free methods for the social sciences. Monterey, CA: Brooks/Cole.

Meehl, P. E. (1978). Theoretical risks and tabular asteriks: Sir Karl, Sir Ronald, and the slow progress of soft psychology. Journal of Consulting and Clinical Psychology, 16, 806-834.

Milton, J., & Wiseman, R. (1999). Does psi exist? Lack of replication of an anomalous process of information transfer. Psychological Bulletin, 125, 387-391.

Mischo, J. (1985). Paranormale erfahrungen im traum. Zeitschrift für Parapsychologie und Grenzgebiete der Psychologie, 27, 116-141.

Murray, H. A., & Wheeler, D. R. (1937). A note on the possible clairvoyance of dreams. Journal of Psychology, 3, 309-313.

Oliva, T. A., Desarbo, W. S., Day, D. L., & Jedidi, K. (1987). GEMCAT: A general multivariate methodology for estimating catastrophe models. Behavioral Science, 32, 121-137.

Orme, J. E. (1974). Precognition and time. Journal of the Society for Psychical Research, 47, 351-365.

Palmer, J. (1979). A community mail survey of psychic experiences. Journal of the American Society for Psychical Research, 73, 221-251.

Popper, K. R. (1978). Logik der forschung. Tübingen: Mohr.

Radin, D. I. (1997). The conscious universe: The scientific truth of psychic phenomena. San Francisco, CA: HarperCollins.

Rogers, L. W. (1923). Dreams and premonitions. Chicago: Theo Book Co.

Rhine, L. E. (1954). Frequency and types of experience in spontaneous precognition. Journal of Parapsychology, 18, 93-123.

Ross, C. A., & Joshi, S. (1992). Paranormal experiences in the general population. Journal of Nervous and Mental Disease, 180, 357-361.

Ryback, D., & Sweitzer, L. (1990). Wahrträume. München: Knaur.

Saltmarsh, H. F. (1934). Report on cases of apparent precognition. Proceedings of the Society for Psychical Research, 42, 49-103.

Schredl, M. (1996). Hör auf deine träume. Küttingen: Midena-Verlag.

Schredl, M. (1999a). Die nächtliche traumwelt: Eine einführung in die psychologische traumforschung. Stuttgart: Kohlhammer.

Schredl, M. (1999b). Präkognitive träume: Überblick über die forschung und zusammenhang zum traumerleben. Manuscript submitted for publication.

Schredl, M., & Doll, E. (1997). Autogenic training and dream recall. Perceptual and Motor Skills, 84, 1305-1306.

Schredl, M., & Doll, E. (1998). Emotions in diary dreams. Consciousness and Cognition, 7, 634-646.

Schredl, M., Jochum, S., & Sougoenet, S. (1997). Dream recall, visual memory, and absorption in imaginings. Personality and Individual Differences, 22, 291-292.

Schredl, M., & Montasser, A. (1996-97). Dream recall: State or trait variable? Part II: State factors, investigations and final conclusions. Imagination, Cognition and Personality, 16, 239-261.

Schriever, F. (1987). A 30-year "experiment with time:" Evaluation of an individual case study of precognitive dreams. European Journal of Parapsychology, 7, 49-72.

Smith, M. D. (1992-93). The effect of belief in the paranormal and prior set upon the observation of a “psychic” demonstration. European Journal of Parapsychology, 9, 24-34.

Sondow, N. (1988). The decline of precognized events with the passage of time: Evidence from spontanous dreams. Journal of the American Society for Psychical Research, 82, 33-51.

Stevenson, I. (1961). An example illustrating the criteria and characteristics of precognitive dreams. Journal of the American Society for Psychical Research, 55, 98-103.

Stowell, M. S. (1995). Researching precognitive dreams: A review of past methods, emerging scientific paradigms, and future approaches. Journal of the American Society for Psychical Research, 89, 117-151.

Stowell, M. S. (1997a). Precognitive dreams: A phenomenological study - Part I: Methodology and sample cases. Journal of the American Society for Psychical Research, 91, 163-220.

Stowell, M. S. (1997b). Precognitive dreams: A phenomenological study - Part II: Discussion. Journal of the American Society for Psychical Research, 91, 255-304.

Strauch, I., & Meier, B. (1996). In search of dreams - Results of experimental dream research. Albany: State University of New York Press.

Thalbourne, M. A. (1984). Some correlates of belief in psychical phenomena: A partial replication of the Haraldsson findings. Parapsychological Review, 15, 13-15.

Thalbourne, M. A. (1994). The SPR centenary census: II. The survey of beliefs and experiences. Journal of the Society for Psychical Research, 59, 420-431.

Thom, R. (1975). Structural stability and morphogenesis. New York: Benjamin-Addison-Wesley.

Ullman, M., Krippner, S., & Vaughan, A. (1977). Traumtelepathie (Dream telepathy 1973). Freiburg: Aurum.

Wiseman, R., Jeffreys, C., Smith, M., & Nyman, A. (1999). The psychology of the seance, from experiment to drama. Skeptical Inquirer, 23, 30-32.

Wiseman, R., & Morris, R. L. (1995). Recalling pseudo-psychic demonstrations. British Journal of Psychology, 86, 113-125.

Zeeman, E. (1974). On the unstable behavior of stock exchanges. Journal of Mathematical Economics, 1, 39-49.

[1] We thank Josh Flanders for his assistance in the data collection. Address correspondence to J. Houran at 301 University Court West, Springfield, IL., 62703, USA. Electronic mail may be sent to <rlange3726@aol.com>

[2] We note that recent research by Milton and Wiseman (1999) challenges the robustness of particular types of reported “psi” effects obtained under experimental conditions.