Kurt Lewin’s Dynamical Psychology Revisited and Revised
by
KULLERVO RAINIO
Professor emeritus, Helsinki University
Address: Suursuontie 29 as. 327, FIN-00630 Helsinki
e-mail: kullervo.rainio@pp.inet.fi
Abstract. The aim of this article is to show that the framework of the dynamic psychology -created by Kurt Lewin – although it is 70 years old – can be a very good basis for modern holistic theory of cognition and behavior. An essential new feature in that “neo-Lewinian” theoretical framework – named here Discrete Process Model (DPM) – is the definition of psychic force: it is treated as the probability of a trial from a cognitive state to another. Thus, the strength of the force has an exact measure: that probability. The cognitive course of events is a stochastic process controlled by those probabilities. – Lewin’s brilliant idea to assume certain valence fields which produce psychic forces is made mathematically more exact in DPM. – The model makes possible to derive estimates for the probability distributions of the behavior alternatives – differently from the Lewinian theory, which is deterministic.
Keywords: choice behavior, cognitive trial, discrete model, graph, hodological, holistic, psychic force, valence field.
1. Introduction. Background
It might seem strange to take into examination Kurt Lewin’s conceptual framework of dynamic psychology 70 years after it was published! – Lewin is such a classic figure, particularly in social psychology, that one may assume all essential to be said about his work. It has to be noticed, however, that his principal mathematical (topological) system which is described in detail in his work “The Conceptual Representation and the Measurement of Psychological Forces” in 1938 seems to be left without deep critics and is not developed further. Just in this work, however, Lewin’s genius and the depth and the originality of his thinking come out most strongly. I believe that that work remained rather unknown in the circumstances of war. In that time there was seemingly more use of Lewin’s fundamental analysis of group dynamics and social conflicts while the mathematical construction of psychological conceptual system appeared to be unfamiliar for the “real life”.
The basic finding by Lewin was seemingly very simple, but revolutionized the scientific thinking in psychology. He found that, in the description of behavior (and of cognition), reality needs to be formed and organized in a new way. In psychology, the world needs to be differentiated to such separate states which have meaning to the subject, the psychological process being a locomotion in such a space, i.e., transitions from a meaningful state to another meaningful state. According to Lewin, only these states with meanings have relevance in psychological description. (For example, when we walk, the steps – which are physically clearly observable and measurable – are normally psychologically entirely irrelevant; instead of that, the state of walking with its meanings – the goal of it, the path to be used etc. – is relevant.)
Nowadays it may be difficult to realize what a remarkable jump in thinking Lewin’s view was: to change over from the concrete world of things to the abstract reality of meaningful states.
This deep insight of a ”particular psychological world” was the basis on which Lewin constructed his conceptual system of dynamical psychology trying to reach mathematical exactness, taking on the use of particular the topological (“hodological”) analysis; that suited well to the discrete space description what was needed. Lewin was able to build explaining models for behavior situations and to examine psychic occurrences in a way that was relevant to them.
Lewin’s framework was, however, just a beginning of the new theory construction. There were no possibilities to produce any useful estimation method in his theory. – Why? In some way Lewin was in his thinking dependent on the deterministic viewpoint – as we shall see. Quantum mechanics was not yet broken its predominance in his time. The quantum theory, in principle, allows a non-deterministic or stochastic view of mental states, as well as a superposition of states. We say that this superposition of states in acted on be a Hermitian operator, which, in the terms of quantum physics, acts according to the principle of complementarity. According to our view of complementarity, consciousness applies certain filters (corresponding to mathematical operators) to create a reality of discrete observables. But the primary process, in the unconscious, experiences the unfiltered multiverse, the unus mundus of infinitely branching paths. Before cognition can be understood, one needs to understand precognition. Freud and Jung understood this. Much of modern psychology appears to have forgotten it.
Kurt Lewin’s sudden death 1947 was detrimental for the development of the new dynamical psychology. At that time we had just started to create epoch-making technical discoveries (computers) and constructing stochastic simulation methods and new theoretical models. These strongly induced application of mathematics in behavioral science. The stochastic learning models by William K. Estes (Estes, 1950) and then by Robert Bush and Frederick Mosteller (Bush & Mosteller, 1955) gave impulses to stochastic theory construction in psychology. The quick development of efficient computing gave opportunities to apply totally new calculation methods. Simulation of complicated models which required enormous amount of computations came possible in practice.
We can only guess what new, fruitful possibilities these methods could have opened to Lewin himself in further construction of dynamical psychology. But without Lewin’s genius the development of the basic mathematical concepts did not get sufficient attention in dynamical psychology. Instead of that, the mainstream psychological research was mostly directed to group dynamics. (I had an opportunity to perceive that trend when I was visiting the Group Dynamics Center in Ann Arbor 1956 and participating shortly a graph theoretical seminar led by Dorwin Cartwright and Frank Harary.)
It was rather late during my research work when I found the possibilities to further create the Lewinian system. – I had applied the stochastic learning theory first to sociological issues – to the birth and development of friendship relations in groups (Rainio, 1961, 1962, and 1966. See also Freeman – White – Romney, 1992, pp. 164-167 “Rainio’s Model of Social Interaction” and Wassermann, 1978, p. 811) -- and later to group problem-solving (Rainio, 1966 and 1970). -- About the year 1970 I realised that, in matter of fact, I was reconstructing the Lewinian system using new mathematical tools (Rainio, 1970 and 1983) .
I realized that on the basis of Lewin’s insightful ideas one can create stochastic (indeterministic) models which have – unlike Lewin’s model - estimation power. A good demonstration of this appeared a model of group problem-solving which gives estimates for behavior in Group Maze test (Rainio, 1972, 1986, pp. 167-187, and 2000, pp. 50-85. See also Rainio, 2008, pp. 24-28 and 73-77). But why return again to investigations carried out many decades ago?
The answer will be surprising: Lewin’s basic idea, discrete behavioural space (the use of topological description) contains seemingly much more than psychological aspects of interest. In its new form his conceptual system is, mathematically clearly analogous to the matrix-algebraic quantum mechanics created by Werner Heisenberg. This ultimate result is philosophically extremely interesting. We shall examine this claim briefly in the end of this article (See also: Rainio, 2008 and 2009).
2. Revision of the Lewinian conceptual system (Lewin, 1938)
2.1. Hodological vs. graph representation
The basic invention of Lewin was to introduce a new geometrical framework, a ”hodological space” (”hodos”, a Greek word meaning ”way”) to describe psychological occurrences. Lewin realized clearly that what is relevant in describing the behavior is not the perceived physical changes but the states of individual’s mind which could be separated from each other on the basis of the psychological meaning of the state.
________________________________________________________________________________
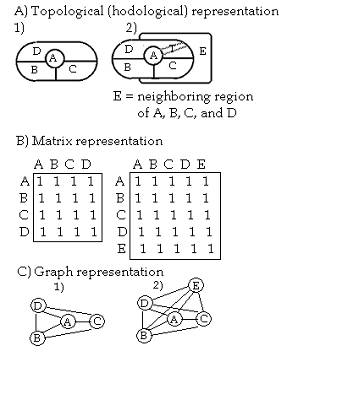
Fig. 1. Topological, matrix, and graph representation of the mind (a life space) as a collection of the states A, B, C, and D (fig. 1A1) , and with E (fig.1A2).

________________________________________________________________________________
”... The purpose of hodological space”, writes Lewin, ”is to find a type of geometry which permits the use of the concept of direction in a manner which will correspond essentially with the meaning that direction has in psychology.” (Lewin, 1938, p. 23)
The hodological space is a discrete presentation of the space. Unlike the Euclidean continuum of points it is constituted of regions with boundaries between them, some regions being ”neighboring” each other (i.e., having common boundaries) some not. The whole of all regions is called ”life space”.
The structure of the ”life space” is defined by the ”neighborhood relation” between the regions. It is conveniently represented in a matrix form - and illustrated by a graph form as exemplified in Fig.1. In fig. 1.A1 the regions A, B, C, and D constitute the life space. Should we add to the life space of A,B,C, and D a new region E as in 1.A2 requiring that E should be a neighbor to all the regions, then we necessarily need in the topological description a new meta-element called a ”tunnel” (T) to connect E and A. The matrix forms of the same life spaces are in Fig. 1.B where the names of rows and columns refer to a ”region” and the element 1 to the existing neighborhood between the row region and the column region. As can be seen from the matrix all regions are neighbors.
From the point of view of theory-building this change is, naturally, trivial.
2.2. Psychological forces
The psychological force is defined effecting in life space, as a cause of locomotion of the point of application (the person) from one region to another.
A force has: 1) direction, 2) strength, and 3) point of application.
According to Lewin, the notation fPA,B means a psychological force effecting in the region A, and having the direction from A to B, and P being as the point of application (Lewin, 1938, p. 83, Fig. 2).
Lewin uses notation ½fA,B½ for the strength of the force.
Usually the meaning of the point of application seems clear from the context. It is a person (as a whole) located in a region and according to Lewin the force influencing the behavior of P can be expressed by notation fP,B as well as fPA,B. However, we shall see later that this is a foggy point in Lewin’s thinking.
Lewin recognizes 3 types of forces (see Fig. 2):
________________________________________________________________________________
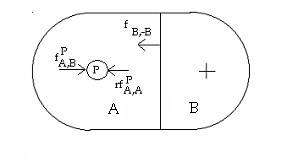
Fig. 2. Life space of the regions A and B and forces acting on person P in A.
________________________________________________________________________________
1) Driving force, notated as dfPA,B if needed – or simply fA,B. It is a force applied to person P, located in the region A, driving him toward the region B.
2) Restraining force, notated as rfPA,A if needed, or simply fA,A. It forces the person P to stay on the same region A where he is already located. Thus, it opposes the driving forces.
3) Boundary force, notated as fB,-B , is acting on the person in order to prevent the person enter the region B when he is in the ”boundary region”. It ”corresponds to the tendency to locomote from B to a region X outside B, for instance to A. The force fB,-B exists, therefore, at least at the common boundary of A and B” (Lewin, 1938, p. 75). When Lewin uses this concept he seems to think that there exists an obstacle between the regions. However, it seems to me strange to see this obstacle as an active force, particularly so because the boundary is not a region. - The concept of boundary force needs clarification – as we shall see.
An essential concept is the resultant force, which Lewin denotes by f*. The resultant force determines the direction of locomotion. Therefore it is extremely important to show how the resultant is derived from the totality of forces empowered in the person. Lewin does not succeed in this. He gives a definition of ”totality of forces” in a region A region A by the following formula:
SfA,X º fA,B + fA,C + ... + fA,N
Lewin gives no clear definition of how to get the resultant force as a sum of its components. He writes about the direction of the resultant force: ”The resultant of a group of forces can have the same direction as one force of the group. ... For instance, it might be that SfA,X º fA,B + fA,C + ... + fA,N = f*A,B .” (Lewin, 1938, p. 85)
In connection to the resultant force Lewin introduces a measure for the speed of locomotion, namely the concept of velocity. If there exists a resultant force f*A,B, directed from A to B and its strength is ½f*A,B½>0, then the velocity of locomotion is also > 0, and notated with vA,B > 0.
As far as I can see, Lewin thinks that the resultant force is the largest of the forces acting in the same time in the same region. According to him, in a certain situation there is one possible resultant force and the behavior could be exactly determined if this could be found out. But Lewin did not have such a method. According to him, a resultant force f*PA,B had appeared ex-ante if a locomotion from A to B was observed. He shows no method to estimate beforehand which direction the locomotion will take. This ruins the usefulness of Lewin’s system as an experimentally testable theory. This weakness in the system is understandable only on that ground that Lewin actually tries to create a deterministic theory of behavior and, thus, as we now well understand, was doomed to failure in his attempt. A radical change at this essential point is necessary.
It is necessary to leave out the concept of a resultant force. The ”psychological forces” should be represented as probabilities of cognitive trials.
To make the use of probabilities possible we shall handle also the time variable as discrete, in addition to the discrete space. The probability of an event will, thus, always mean the probability per a given unit of time - one step of the process taken to run in one unit of time measure.
The ”psychological force” as a propensity to make a trial to change the prevailing state or preserve it during one step in time, and the propensity measured with the probability measure offers a more sound and flexible theory of dynamic psychology. The greater the propensity the greater the probability and also the psychological force involved. The strength and direction of a force are both implicitly determined by the probabilities of locomotion to adjacent regions. These probabilities capture the meanings of the Lewinian driving forces fA,X , and the probability to stay fully captures the meaning of the Lewinian force fA,A.
The direction of ”locomotion”, i.e., the trial alternative, is then determined with a “lottery” outcome from a probabilistic choice using the vector of the trial probabilities applicable to the situation concerned.
An example of this correction is shown in Fig. 3.
In this very important revision the original Lewinian system loses its deterministic character and we shall be dealing with a stochastic theory. This gives an opportunity to use the revised theory also for estimation purposes.
________________________________________________________________________________
Fig. 3. Resultant force concept
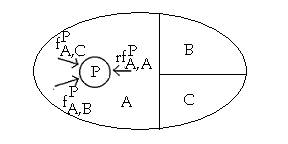
Lewin: Driving forces fPA,B and fPA,C ; restraining force rfPA,A ; resultant force f*PA,B.
Correction: Vector pA,X
Pr[A,B] driving force
Pr[A,C] driving force
Pr[A,A] restraining force
(No resultant force. Probabilistic choice using vector pA,X determines the locomotion.)
________________________________________________________________________________
2.3. Boundary of a region. Barrier strength
The concept ”strength of a barrier” by Lewin has nothing to do with the boundaries of topological (or hodological) representation. (See Fig. 4) The “barrier” has an illustrative character only.
________________________________________________________________________________
Fig. 4. Barrier strength
Lewinian description; example:

Correction using probabilities of the non-success of trials:
Column vectors:
A B C D
A, psucc é1 ù é.9ù é0 ù é0 ù
“, pØsucc ë0 û ë.1û ë1 û ë1 û “strengths of barriers”
B, psucc é.8 ù é1 ù é.6 ù é0 ù
“, pØsucc ë.2 û ë0 û ë.4 û ë1 û “strengths of barriers”
C, psucc é0 ù é.5ù é1 ù é.3 ù
“, pØsucc ë1 û ë.5û ë0 û ë.7 û “strengths of barriers”
D, psucc é0 ù é0 ù é.6 ù é1 ù
“, pØsucc ë1 û ë1 û ë.4 û ë0 û “strengths of barriers”
The non-success probabilities of trials (bold numbers) indicate the “strengths of the barriers” (in the Lewinian terms). Thus, the non-success probability “1” means an “impassable barrier”.
________________________________________________________________________________
However, Lewin seems to have touched here, intuitively, on an important topic, the resistance of the psychic locomotion. But one can ask why he has not applied the idea more systematically to all boundaries between the regions.
It seems convenient to define - in analogy to the strength of a barrier - a particular concept of probability of the success of a trial and apply it to all the relations between the neighboring regions (graph nodes). Thus, the ”strength of the barrier” will now have a new, mathematically exact meaning: it is defined by the probabilities of success of cognitive trial – inversely: i.e., the strength of the barrier gets its minimum value when the success probability is one and maximum when it is zero. (The success probability of cognitive trial varies according to learning experiences.)
The transition from a behavioral state to another (subject’s real action) is also dependent of its success probability. The behavior success is, however, a property of environment (success of a move in game etc.) Thus, no learning is applied to the probabilities of the behavioural success.
2.4. Point of application of forces. Group behavior
Lewin emphasizes in his work the need to see the individual as a whole in analyzing the psychological situation. Thus,”the point of application of forces” in Lewin’s representation is the person. Lewin shows this applying a special superscript symbol P with the symbol of force fPA,B . Lewin uses also a shortened expression fP,B instead of fPX,B where X indicates any of the regions. Lewin writes: “If we wish to indicate specifically the point of application we will write: fPA,C where A represents the region where the force exists, dA,C the direction of the force and P the point of application. We will not indicate specifically in our formulas the point of application when the meaning is clear.” (Lewin, 1938, p. 74)
Lewin seems to forget it in his discussion of the ”inner personality”, particularly in his presentation of a ”relation between a force for locomotion acting on the person as a
whole and the tension in inner systems”. (Lewin, 1938, p. 98). He uses in this context, e.g., the expression
![]()
indicating ”a force working on the boundary b of S in the direction of the neighboring system S1 ” (Lewin, 1938, p. 99). Which is now the ”point of application of forces”? If it is an ”inner system” of a person, is it meaningful to discuss the ”life space” of such a partial system?
It seems to me that, in omitting the problem of point of application of forces, Lewin commits a mismatch. – Some ”group dynamists” are guilty of the same kind of a logical mismatch or an ”inventory error” when they take forces to act at the same time both on the group and on the members of that group.
For solving the formal problem and for avoiding the confusion, the ”life spaces” of different subjects should be kept logically separate from each other. But the subjects may yet interact with each others, which means that the forces involved are then given as conditional probabilities, the conditioned by the expectations concerning the behaviour of the other group members. The point of application is always an individual.
2.5. Force field and its valence
The origin of a force is, according to Lewin, a specific characteristic of region (a mind state), which he calls the valence of it. Lewin gives the definition:
”A region G which has a valence Va(G) is defined as a region within the life space of an individual P which attracts or repulses this individual. In other words:
Definition of positive valence:
If Va(G) > 0, then ½fP,G½ > 0.”
”Definition of negative valence:
If Va(G) < 0 then ½fP, - G½ > 0.”
Lewin continues: ”The concept of valence ... does not imply any specific statement concerning the origin of the attractiveness or the repulsiveness of the valence. The valence might be due to a state of hunger, to emotional attachment, or to social constellation... The statement that a certain region of the life space has a positive or negative valence merely indicates that, for whatever reason, at the present time and for this specific individual a tendency exists to act in the direction toward this region or away from it.” (Lewin, 1938, p. 88)
Lewin makes an assumption which is very essential in his framework: the valence induces a force field which reaches more or less all regions in the life space creating in them a force toward the goal region, G , if G has a positive valence, or away from G, if the valence of G is negative. – ”As in physics, the forces of a force field are only conditional ones; they are those forces which would exist in a region if the individual should be located in this region.” (Lewin, 1938, p. 90)
Lewin illustrates the force fields by figures indicating the forces by arrows[i]. The figure representing positive central force field is reproduced in Fig. 5. One can see that there is no exact theory but an illustration in question.
________________________________________________________________________________
Fig. 5. “Positive central force field corresponding to a positive valence (Va>0)” (Lewin, fig. 33)

“G, region of a positive valence (Va(G)>0), located in C; P, person; the forces fA,C , fH,C, or fL,C correspond to Va(G) in case P is located at A, H, or L, respectively; fX,Y = fX,G .”
________________________________________________________________________________
Lewin’s representation of force field is not exact. Later in this article (Chapter 4.3) it will be shown that the Lewin’s invention of valence is in a modified probabilistic form a very suitable concept for the description of intentional activity and goal-directed behavior.
Later, in Chapter 4.3, we shall handle the valences and the potencies of fields further and see how the trial probabilities (forces) are derived from them in an exact way.
2.6. Cognitive and behavioral (“real”) world
Lewin’s representation has a confusing tendency to describe sometimes cognitive phenomena and sometimes the so-called ”reality” by using the same terms and without formally making any clear distinction between them. In order to create an exact theory, it is, however, quite necessary to make this distinction, as clearly as possible.
In the “Discrete Process Model” (DPM) as I should call the theory-model that will be described later in this article more systematically, the psychic processes will be presented as occurring, naturally, in the cognitive space. The ”regions” (nodes in our graph representation) stand for cognitive states of the subject. The psychic forces act always and only on a cognitive state - activating cognitive trials in order to change or preserve the state.
The graph representation (as well as the matrix representation of transition probabilities) is used also for the ”real” world (i.e., for the world seen as well by the subject as by an observer and interpreted according to the psychological relevance). Thus the “objective” states of an individual are represented as nodes of a graph but this representation has no a priori linkage to the cognitive world of the person in question.
The linkage is given by a particular concept of correspondence, i.e., in the form of a correspondence probability matrix where the rows indicate cognitive states, the columns real world states, and the elements the probabilities of the correspondence between these states.
The correspondence probabilities may vary between 0 and 1. It is, however, plausible to assume that usually, for instance in game situations with clearly defined rules, the probabilities might well equal to 1 or 0.
Actually we have to take in our use two kind of correspondence matrices:
1) RCC - (reality-cognition) -correspondences, probabilities indicating which ”cognitive map” corresponds to a certain real situation.
2) CRC - (cognition-reality) -correspondence, probabilities indicating which is the real state to which the subject’s certain cognitive state refers, e.g., which behavior movement follows a certain decision to move.
The essential difference between the original Lewinian framework and the “neo-Lewinian” Discrete Process Model (DPM) is that the latter offers the possibility to measure the variables such as the strength of psychological force, the strength of barrier, and the strength of valence in terms of probabilities. Thus, the DPM-framework may be worth a more systematic, brief, summarizing description.
3. Discrete Process Model. Basic concepts
(Rainio, 2008)
In our theory, both space and time appear as discrete variables.
At any point in time, the person is assumed to be in one and only one state defined in the discrete space. In any time-step the person transits from an actual (cognitive or behavioural) state to another one or stays in the prevailing state. In principle, any transition between the states is possible. It is assumed, however, that there exist conditional probabilities of transitions from a given state. (Staying in the prevailing state is one alternative among the transitions and occurs by a certain probability, too.)
The transition principle is applied separately in cognitive and behavior occurrences.
The basic concepts and symbol notations are as follows:
Symbol: Verbal description:
Behavior:
Be(i,a,t) Behavior state: an individual i maintains a behavior state a at the moment t – in other words: i is in the real behavior state a in a space of states at t, i.e., Be(i,a,t) Î{Be(i,x,t)}.
Symbol: Verbal description:
By the ”real behavior state” we mean a psychologically relevant situation of an individual, available for observation, in principle.
Tr(i,a,b,t) Behavior trial: it is a try to change a behavior state maintained, i.e., i,
being in the state a, tries to behave in the way b at the
time point t.
Succ(i,a,b,t) Success of the trial, a shortened expression of Succ(Tr(i,a,b,t)).
Correspondingly, ¬Succ(i,a,b,t) means failure of the trial Tr(i,a,b,t).
Cognition:
(Notice the sign ‘ indicating cognitive things.)
C(i,a’,t’) Cognitive state: i imagines in the way a’ at a cognitive time point t’ – in other words: i is in the state a’ in the space of cognitive states at the cognitive time point t’. And C(i,a’,t’) Î { C(i,x’,t’)}.
Tr’(i,a’,b’,t’) Cognitive trial: i whose cognitive state is a’, tries to make a cognitive
choice b’ at the cognitive time point t’.
Succ’(i,a’,b’,t’) Success of a cognitive trial Tr’(i,a’,b’,t’). ¬Succ’ means the failure.
NS’(i,a0’,b’,t) Cognitive success sum: number of consecutive successful cognitive trials
made by i toward b’ from the state a0’ at real time point t.
AT(i) Action threshold: an integer indicating the number of consecutive
successful cognitive trials (NS’) needed to make a decision and to start an
action (a “real” trial) according to it.
Cognition and reality:
RCCor(i,a,M’,t) Reality-cognition correspondence: i, being in a behavioral state a at the
time point t, creates in his cognition a cognitive map M’ (Life Space) which
consists of the relative cognitive states in the actual situation a.
The cognitive map resembles, for its structure, the graph of the real states but need not to be identical with it. In a problem-solving situation, where i commits himself to the rules of the problem, the cognitive states of M’ may well be in one-to-one relation to the real states.
CRCor(i,a’,a,t) Cognition-reality correspondence: in i’s cognition, the cognitive
alternative a’ corresponds to the behavior alternative a at the moment t.
The correspondence between individual’s cognition and the behavior space is given by probabilities p(CRCor(i,x’,x,t)).
(In laboratory game situations it is usually plausible to assume the simplified one-to-one relation, i.e., there is always for every x’ one and only one x corresponding to it.)
Cognitive and real time:
Real time points are denoted by t, t+1, t+2 etc. Analogously, t’, t’+1, t’+2
etc. indicate points in cognitive time. If the cognitive time-step is denoted
by Dt’ and behavioral time-step by Dt then Dt’ £ Dt.
Cognitive information in the mind (I), according to Germine (1993), can, in principle, be determined by the frequency of state changes (P), the probability of the state (R) from 0 to 1 (relative entropy), the total of possible microstates (g), and Boltzman’s Constant (k) according to the equation:
I = (1-R) k Pt ln g
In this model, a superposition of states could be said to exist, each with a certain probability, with a higher information content associated with realization of a lower probability state. The superposition of states would then be the sum of the fields. The function g can be viewed abstractly as the area of the life space in Lewinian terms. The transition from one state to the next may be viewed is collapse of the wavefunction, which would presumable be the entirety of the life space at a given time, into a single region of the life space. The movement involved would then involve a path in hodological space.
4. The cognitive process and behavior according to the DPM
4.1. Cognitive and behavior transitions
Lewin described the psychological process as locomotion of the person from a region to another in topological space. The direction of locomotion was determined by the resultant force. Lewin did not make any distinction between the cognitive and behavior locomotion. DPM makes this distinction. According to it, there occur cognitive transitions from a cognitive (mental) state to another and behavior transitions from a behavior (observable) state to another. The direction of a transition is determined by transition probability vector and by a probabilistic choice using it. (In simulation of the process, Monte-Carlo –method is applied.)
The main features of the cognitive process and of the first behavior choice are given in the following “flow chart” list (Table 1). (The topological structure – the graph – of the Life Space and the corresponding “cognitive map” – cognitive Life Space – are assumed to be set in the beginning.)
Table 1 shows the cognitive steps needed for one behavior transition. (For the sake of simplification, action threshold AT(i) is assumed to be 1.)
________________________________________________________________________________
Table 1. Cognitive process and the first behavior choice. “Flow-chart”.
1) Start. – Give to the state-variable x the value x0 and to the time-variable t the value t0 .
Thus, the behavior state is Be(i, x0 ,t0 ).
2) Give to the cognitive time-variable t’ the value t0’ and to the cognitive state-variable x’ the value x0 ’.
Thus, the cognitive state is C(i, x0’,t0’).
3) Determine the cognitive trial Tr’(i,x0’,yk’,t’), applying the Monte-Carlo-method to the probability vector p(y’½x0’) and denote the outcome by yi’. – Add 1 to t’.
4) Determine the success of the cognitive trial, applying the Monte-Carlo-method to the probability vector p(succ’(Tr’(i,x0’,yi’,t’))), the outcome being succ’(Tr’(i,x0’,yi’,t’) or ¬succ’(Tr’(i,x0’,yi’,t’).
5) Test the outcome of the success of the cognitive trial.
6) If ¬succ’ then go to 3
7) If succ’ then set yi as an argument of the real trial Tr(i,x0,yi,t) – x0 corresponding to x0’ and yi to yi’.
8) Determine the success of real trial Tr(i,x0,yi,t), outcome being succ (Tr(i,x0,yi,t) or ¬succ Tr(i,x0,yi,t). Carry out learning.
9) If ¬succ then go to 11.
10) If succ then set yi in the real behavior Be(i,yi,t+1) and go to end (12).
11) Let tn indicate the end of time available. – Test t. If t < tn then set x’, y’, and t0’ and go to 3 but if t = tn then no action occurs and go to end (12).
12) End.
________________________________________________________________________________
4.2. Learning
DPM offers an easy way to mathematically take the learning phenomenon into account. We may well assume learning reinforcement so that 1) the success of trial affects the cognitive trial probabilities rewardingly, the failure having a punishing effect and 2) the reached real state has the quality of producing reward or punishment concerning both the trial probabilities and the success probabilities. We can apply some stochastic learning model, e.g., the Bush-Mosteller’s Two Operator Learning Model (Bush and Mosteller, 1955).
An example: Let’s assume a cognitive trial probability vector F:
F
A’ B’ C’ D’ S
A’ (.2 .5 .2 .1) 1
If the Monte Carlo –lottery has given the outcome C’ and, thus, the person makes the trial from A’ to C’ and, further, it is assumed that this C’ state happens to be rewarding and the trial successful; then the rewarding Bush-Mosteller operator is applied. This means that the cognitive trial probability toward the state C’ increases according to the equation:
pt+1 = pt + a(1 – pt )
Suppose that the learning coefficient a = .5; the equation gives the new trial probability pt+1 toward the state C’. It is .2 + .5(1-.2) = .6. The other elements of the vector
need to be decreased so that the sum equals 1. Thus, the new trial probability vector is:
(.1 .25 .6 .05) S=1
The same learning principle is applied to the probabilities of the success of the cognitive trials, too.
4.3. Valence, field and potency of field
One of the great inventions of Kurt Lewin was to borrow the concepts of force field from the physics and apply it with a concept valence to psychological life space. The fields organize the life space. The valence gives to a field (Lewin: region) its goal character.
However, as we have seen in Chapter 2.5, Lewin used the concepts of field and of valence mostly in an illustrative way. The new, more specified definitions of those concepts will be given in the following.
A field, in DPM, is identified or defined by a subgroup of states within the LS. The field partitions the life space LS into two subspaces: the states belonging to the field (F) and the states outside F denoted as (ØF).
All fields in DPM description are cognitive. – There may exist none, one or more states as elements of a field. A state may be an element in many fields; thus, the fields may be distinct or overlapping.
The whole ”life space” itself is a field. This field (FLS or simply LS) includes, then, all the relevant cognitive states as its elements (ØLS being an empty subspace).
An example of 3 fields in LS is given in Fig. 6.
________________________________________________________________________________
Fig. 6. Three fields in LS
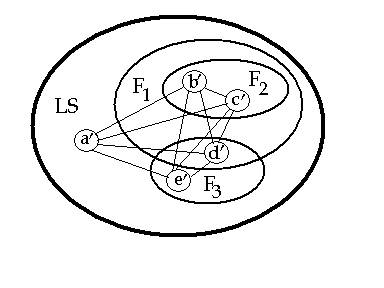
LS = {a’, b’, c’, d’, e’} ØLS = {empty}
F1 = {b’, c’, d’} ØF1 = {a’, e’}
F2 = {b’, c’} ØF2 = {a’, d’, e’}
F3 = {d’, e’} ØF3 = {a’, b’, c’}
Notice that F2 is included in F1 but F3 not, and that fields F2 and F3
are distinct but F1 and F3 overlapping – the intersection being d’.
________________________________________________________________________________
Definition of valence and its measure:
Lewin gives actually no exact measure for the valence: according to him there are only positive and negative categories of valences. The new measure of psychological force in terms of the trial probability gives an opportunity to define the measure of valence.
If there exists a field F with a valence in the life space LS, the field F partitions the states of LS into two groups:
F = {s1, s2, … , sn } , the field including states from s1 to sn in LS, and
ØF = all the other states, i.e., states of LS not belonging to the field F.
We define the measure of valence of the field as follows :
There are 4 “field forces” induced by the field; they form the following probability matrix:
F ØF S
F épF,F pF,ØF ù 1
ØF ëpØF,F pØ,F,ØF û 1
An example in a matrix form and in an illustrative graph form is given in Fig. 7.
In the example in Fig. 7 there are only two states, one inside F and the other outside it. Thus, pF,F needs to be equal to pb,b , pF,ØF to pb,a etc. What the “field forces” generally mean in terms of cognitive trial probabilities will be presented later.
________________________________________________________________________________
Fig.7 . Life Space including one field F and two states a and b. Forces produced by the field F
“Field forces”

The “field force pF,F is acting as a “restraining force” pb,b , the strength of which is assumed to be .9, while pF,ØF (strength .1) is acting as a “driving force” pb,a from b to a, pØF,F (strength .8) as a “driving force” pa,b from a to b, and pØ,F,ØF (strength .2) as a “restraining force” pa,a.
________________________________________________________________________________
According to Lewin, if the field G has a positive valence, there must exist a force ½fP,G½>0; if the field G has a negative valence, there will exist, correspondingly, a force ½fP,-G½ > 0. (Lewin, 1938, p. 88, statements 20 and 20a)
Both definitions of the valence are too narrow. Using the “field force” probabilities above, we can define the valences more completely:
Va(F) = [(pF,F – pF,ØF) + (pØF,F - pØF,ØF)]/2
The equation gives the maximum positive value 1, if pF,F = 1 and pØF,F = 1 and the maximum negative value -1, if they both are 0. – In the example in Fig. 7 , the measure of valence is: [(0.9 - 0.1)+(0.8 - 0.2)]/2 = 0.7.
The field’s effect on the cognitive trial probabilities. Potency of field
The fields produce the psychological forces acting on states. If there exist no fields inside the Life Space, the LS is homogeneous, i.e., all forces have equal strength (probability) and each trial probability is 1/n , n indicating the number of states in LS.
If there are one or more fields in LS, we have to combine the effects of them for deriving the strengths of the forces, the trial probabilities. This will be done by giving certain weights to the fields in the following way:
We use the term potency of a field to indicate the weights used in combining (summing up) the effects of the fields in calculation of the cognitive trial probabilities. Thus, the sum of the potencies has to be 1. – The rule of the calculation is following:
Let’s matrix pF indicate the 4 field forces produced by a field F.
pF
F ¬F
F épF,F pF,ØF ù
¬F ëpØF,F pØF,ØF û
Suppose that there are nF states inside the field F and nØF outside it. It seems plausible to assume that the force pF,F is distributed equally to the states inside the F, the force pF,ØF equally to the states outside F, the force pØF,F equally to the states inside F, and the force pØF,ØF equally to the states outside F.
The general equation for this calculation is given in Rainio 2000, Chapter 2.6. We examine here (Table 2) only a numerical example calculating the trial probabilities according to Fig. 6. We make a simplification and assume that the valences of all the fields are = +1. The potencies are given in Table 2, too.
After calculating the component vectors we shall form a weighted sum of them using potencies of the fields as weights. These weighted sums are, thus, the trial probabilities.
________________________________________________________________________________
Table 2. Computing the trial probabilities produced by fields
(See the example in Fig. 6)
Fields nF Vectors of probabilities Potencies
a’ b’ c’ d’ e’
LS 5 a’ (.2 .2 .2 .2 .2) .1
F1 3 a’ (0 .33 .33 .33 0 ) .3
F2 2 a’ (0 .5 .5 0 0 ) .4
F3 2 a’ (0 0 0 .5 .5) .2
Components weighted by potencies:
LS a’ (.02 .02 .02 .02 .02)
F1 a’ (0 .1 .1 .1 0 )
F2 a’ (0 .2 .2 0 0 )
F3 a’ (0 0 0 .1 .1)
Sums, the trial
probabilities
(“driving forces”): a’ (.02 .32 .32 .22 .12) S @ 1
(The trial probability vectors b’, c’, d’, and e’ are equal to a’.)
________________________________________________________________________________
Note: The high potencies of fields F1 , F2 , and F3 (in the example in Table 2) mean psychologically high differentiation of cognition. If they were low and Pot(LS), correspondingly, high, the cognition would be undifferentiated, diffuse. The extreme case while Pot(LS) = 1 and, thus, all trial probability vectors (“forces”) (.2, .2, .2, .2, .2) , would indicate the most primitive cognition, “random walk” through the states. – (The “picking up” the relevant states, giving form to the actual life space, means, naturally, the first and most fundamental differentiating act of subject.)
Lewin talks about some concrete things which can produce valence fields, e.g., food, social acceptance, producing something valuable, electric shock (negative field) etc. – We emphasize, however, the cognitive aspect: cognitively, the goals (or cognitive states having valence) mean that those states are bringing positive expectations. (Correspondingly, the state with negative valence creates negative expectations which lead to the avoidance of it.) Not until the goal is reached (i.e., the corresponding behavior trial occurs and succeeds), a learning reinforcement takes place. – The goal needs not to be a “real thing”; it can well be a cognitive state, e.g., during a thinking process a state where the individual experiences that the problem is solved. This can produce – without any “outer behavior” – a reinforcement effect, too.
The expectations play an essential role in group dynamics. According to DPM, the group is defined as a set of individuals (members) who have at least one expectation concerning the behavior of some other member. This makes every individual in that set of individuals somehow dependent on the others. In human groups the expectations are strengthened by communication. The expectations are definite, if the person believes completely the message he receives, otherwise he does not take the message into account; thus, a probability vector is used for determining the believing. (Seemingly, there are cultural differences: if in a group – or in a culture – the probabilities to believe the messages are high, the group behavior is more articulated (differentiated) than in groups with low belief probabilities.)
The analysis of group behavior is not examined here further. (A detailed description of group behavior – in terms of DPM – is available in Rainio 1972 and 2000.)
5. Discussion
Although very little empirical work has been done using Discrete Process Model for estimation, some laboratory experiments show that the model can well be operationalized at least in well controlled laboratory game situations; in those situations, namely, the behavior choices and communication acts are observable. A particular Group Maze experiment has been constructed and simulated using DPM. The goodness-of-fit of the simulations has been rather high (Rainio, 1972 and 2000).
Physical quantum mechanics and DPM:
The mathematical structure of DPM is general; it covers different kinds of systems. Thus, it is actually not very surprising that it is applicable to the description of physical quantum evolution, too.
The probability of cognitive trial corresponds – in quantum mechanics – to the probability of transition of a system from one quantum state to another. (But no “success” of transition is assumed.) The vector of the transition probabilities at a certain point in time indicates a system’s superposition state. This corresponds to Feynman’s sum over all paths. The system’s evolution process is manifested as “jumps” from a superposition state to another. If some vector, however, allows only the staying in the actual state (i.e., the transition probability from the state i to itself, pi,i , is 1 and the others 0), then the process ends in this stable state. Such a state is not a superposition state but a so-called “definite” state and it is observable, in principle – i.e., the system exists in that state.
The application of DPM both to physical quantum mechanics and to cognition is represented in detail in Rainio’s several works (Rainio, 2008 and 2009). Notice that, independently of DPM and without knowing it, McCall, Whitaker, and George have also used a discrete quantum evolution model which is based on the transition probabilities (McCall, Whitaker, and George, 2001).
It is philosophically interesting and important that the DPM approach – being extremely abstract and general – seems to be able to combine the quantum mechanical theory and the dynamical psychology to the same conceptual framework. (One has to notice, however, that the dynamical psychology is not identical with whole psychology.) This framework seems to open a possibility to find a plausible ontological solution to the mind/body problem (Rainio, 2008 and 2009). It brings also certain exactness into the implicate-explicate order construction by David Bohm (Hiley and Pylkkänen, 2005, and Pylkkänen, 2007). Because DPM shows that the theory of physical and conscious processes are derivable from the same mathematical structure – which has the characteristics of field of “active information” (Bohm) – DPM seems to represent information monism. This term is used by Dan Kurth (Kurth, 2007, p. 27) in the form “information monism” and Mark Germine in the form “information monism”. Germine writes (Germine, 2007): ”Wheeler has said that all of reality is information, and that other physical quantities are ‘merely incidentals’. Information monism is gaining popularity in physics.”
It seems obvious that Kurt Lewin’s brilliant intuitive insights concealed fundamental ideas which lead to new understanding not only in dynamical psychology but also in a much greater domain of philosophy.
Acknowledgement
I am very grateful to many members of the Finnish Society of Natural Philosophy for their interest in my ideas and I want to thank particularly Pentti Malaska – emeritus professor in mathematics of economy and honorary doctor in technology – who has been patiently great help to me.
References
Bush, Robert R. and Mosteller, Frederick (1955): Stochastic Models for learning. New York,
Wiley, 1955.
Estes, William K. (1950): Towards a Statistical Theory of Learning. Psychological Review
57: 94-107.
Freeman, Linton C., White, Douglas R., Romney, Kimball (1992): Research Methods in
Social Network Analysis. [Rainio’s Model of Social Interaction, pp. 164-167.]
Germine, M. (1993): Information and Psychopathoogy. Journal of Nervous and Mental
Disease 181: 382-387.
Germine, Mark (2007): The Holographic Principle Theory of Mind.
http://www.goertzel.org/dynapsyc/2007/holomind.htm
Hiley, Basil and Pylkkänen, Paavo (2005): Can Mind Affect Matter Via Active
Information? Mind and Matter, Vol. 3(2), pp. 7 – 27.
Kurth, Dan (2007): An Interpretation of QM Based on the Holographic Principle and M-
Cosmology. The IGN Preprint Series, No 35, Aug. 2003.
http://web.uni-frankfurt.de/fb15/prep/ANPA03Paper.pdf
Lewin, Kurt (1938): The Conceptual Representation and the Measurement of Psychological
Forces. Contributions to Psychological Theory, 4, Duke University Press, Durham, N.C.,
1938.
McCall, Storrs – Whitaker, Andrew – George, Glyn (2001): Continuous vs Discrete
Processes: the Probabilistic Evolution of Single Trapped Ions. Paper presented at the
10th UK Conference on the Foundations of Physics, Belfast, 2001. Full text:
http://philsci-archive/pitt.edu/archive/00000521/
Pylkkänen, Paavo (2007): Mind, Matter and the Implicate Order. Springer Verlag. The
Frontiers Collection. Berlin - Heidelberg, 2007.
Rainio, Kullervo (1961): Stochastic Process of Social Contacts. Scandinavian Journal of
Psychology, pp. 113-128.
Rainio, Kullervo (1962): A Stochastic Theory of Social Contacts; A Laboratory Study and
an Application to Sociometry. Transactions of the Westermarck Society VIII, 101 pages.
Rainio, Kullervo (1966): A Study on Sociometric Group Structure, in Berger, Zelditch,
and Anderson (eds.): Sociological Theories in Progress. Boston, Houghton Mifflin, 1966
Rainio, Kullervo (1970): The Conceptual Representation of Choice Behavior and Social
Interaction, Quality and Quantity, IV, pp. 165-192. 1970
Rainio, Kullervo (1972): Group Maze. Experiments and Simulations in Problem-Solving
by Groups. Commentationes Scientiarum Socialium, 3. Societas Scientiarum
Fennica, Helsinki.
Rainio, Kullervo (1983): Corrected Lewinian System in Terms of Probabilistic Theory, in
Micko and Schultz (eds.): Formalization of Psychological Theories. University of
Bielefeld.
Rainio, Kullervo (1986): Stochastic Field Theory of Behavior. Commentationes Scientiarum
Socialium, 34. Societas Scientiarum Fennica, Helsinki.
Rainio, Kullervo (2000): Cognitive Process and Behavior; A Conceptual Framework and
Simulations. Research Reports 1/2000, Department of Social Psychology, Helsinki
University. e-book, whole text available in address:
http://ethesis.helsinki.fi/julkaisut/val/sosps/muut/rainio/
Rainio, Kullervo (2008): Discrete Process Model for Quantum and Mind Systems.
Research Reports 1/2008, Department of Social Psychology, Helsinki University. e-book,
whole text available in address:
http://ethesis.helsinki.fi/julkaisut/val/sosps/muut/rainio2/
Rainio, Kullervo (2009): Discrete Process Model for Quantum Systems of Matter and Mind.
World Futures, Vol. 65, Issue 4 May 2009, pp. 270-303.
Wassermann, S.S. (1978): Models for Binary Directed Graphs and Their Application. Adv.
Appl. Prob. 10, 803-818.