In Search of the Universal Equation

String Theory, Subatomic Computing, and other Bold Attempts

to Form a Unified Picture of the Submicroscopic World

of which our Universe is but a Shadow

Ben Goertzel

July 6, 2001

Science has proved Plato’s parable of the cave true in more ways, and in richer detail, than its author could have imagined. He had the unchanging essence of mind and world down pat. Today, as in ancient Greece, we’re all still basically sitting here in a cave, our backs toward the cave mouth, watching the shadows of trees and birds and bears dance on the cave’s back wall, taking the shadows for the reality because we’re unable to see the real world outside. This is the lot of all finite minds, and always will be – thus was Plato’s intuition. But what he couldn’t see was what a complex combination of experimental tools and mathematical and conceptual theories we would conceive, describing one after another aspect of this real world we cannot see – never perfectly, but better and better as time goes on, converging toward the infinite limit of real understanding, a limit that will never be reached.

Cognitive neuroscience shows us that the cave extends even into ourselves. The mind we perceive is not the actual mind that controls us. We believe our conscious decisions are controlling our actions, but underneath, most decisions arise prior to the conscious process that believes it originates them, as a result of the self-organizing combination of millions of microscopic neural events.

Quantum physics shows us that even the most apparently solid and simple phenomenon of physical reality is just a shadow dancing on the wall. All of us, all the objects around us, are really far more than 99.99% empty space. The idea that anything has a definite position, mass or speed is an illusion: at bottom everything is made of particles whose state is fundamentally indeterminate. The shadow world looks determinate and solid, until you look at it closely, then you see that the real world reflected in the shadows is indeterminate and fuzzy, and this indeterminacy is important for understanding some aspects of everyday things. The genes and proteins that guide our body rely on quantum mechanical phenomena in their every interaction. You can’t understand them by thinking about the immediately perceptible world, the shadows on the wall – rather, you have to use what we’ve learned about the world behind the shadows, as bizarre and counterintuitive as this world has come out to be.

And our investigations into the world behind the shadows gets stranger and stranger as time goes on. Indeed our minds, adapted to the phenomenal world, stretch to grasp these new insights. It is quite remarkable how science, itself a channeling of the human mind in particular directions, can lead to conclusions that rattle the mind so thoroughly, down to its foundations.

Some of the most dramatic revelations of this kind, in recent years, have come from physics. Quantum theory shows us that the everyday world with its solid objects and definite events is just a shadow world, that the real world underneath is quite different -- and much more confusing, because our brains aren’t adapted to it. The particles we’re made of don’t have definite states, they’re suspended between different conditions of being, and it’s this suspension that, by complex chains of causation, makes it possible for proteins to bind together creating organisms from genes, and for electricity to zip between neurons creating emergent thought-patterns. But quantum theory itself is not complete: it only explains a piece of the shadow-world we see around us. Gravity, which holds us down on the Earth and keeps us from flying into space, is a rather obvious feature of the world around us, yet so far no one has a really good understanding of how quantum theory is consistent with gravity.

To put it another way: Among the shadows we observe on the wall we call the world, are proteins and electrical fields, planets and gravity. We have a theory about how the real world casting the shadows works that explains proteins and electrical fields – this is called quantum physics. We have a theory about how the real world casting the shadows works that explains gravitation – Einstein’s General Theory of Relativity. But these theories, when you get down into the nitty-gritty of them, appear to contradict each other.

And in their efforts to resolve this contradiction, scientists are coming up with yet more complex and peculiar hypotheses about the world behind the shadows. The real universe, hundreds of physicists at esteemed institutions now believe, is a ten-dimensional world made of vibrating strings resonating at different frequencies. But this hypothesis isn’t yet as convincingly proven as quantum physics or gravity. There are alternative theories. Some scientists believe that the real hidden universe isn’t a multidimensional string symphony, but rather a huge invisible computer. We’re all patterns in the universe-computer’s memory, produced by a software program called physical law.

Who’s right? Building multibillion dollar particle accelerators may help us find out. Or it may not. At the moment the string theory’s most interesting concrete predictions involve the behaviors of certain types of black holes – interesting predictions, but hard to test given the current state of practical astronomy. These lines of scientific research may lead to the technology of the next century: superpowerful atomic-scale computers, even faster-than-light travel or time travel. Or they may just lead to a lot of difficult and expensive head-banging against the wall of unsolvable mathematical equations and experimental predictions unverifiable in practice.

From a very general perspective, though, one thing seems clear. Some journalists and a handful of scientists have referred to string theory and other advances in modern physics as the search for a “Theory of Everything.” But this phrase is misleading in many ways. Progress in these areas of physics may lead to a lot of exciting things, but a universal understanding of everything is not likely to be one of them! For a number of particular reasons that I’ll discuss a little later, even a universal unified physics theory is likely to leave a huge number of gaps in our understanding of the cosmos. The quest to map out the real world behind our backs, by inferring patterns in the dance of the shadows, is an ongoing one, with periods of apparently stable understanding, periods of confusion, and periods of revolutionary conceptual progress. Modern physics is just another chapter, albeit a fascinating one. The more things change, the more they stay the same.

The History of Physics as a History of Contradictions

The history of physics can be understood as a series of successful attempts to use mathematics to come to grips with the intuitively incomprehensible aspects of the world. Human common sense is tuned for explaining human-scale earthly physical events, but as experimental science progressed, we discovered more and more about the physical world in other places and on other scales. The further our discoveries got from the everyday world, the less useful our common sense was for explaining them. Mathematics, however, is not restricted to describing structures and processes that agree with our common sense. We are able to set up equations and models based on our common sense understanding, and then derive highly counterintuitive conclusions from them. This is the power of mathematics.

Newton, in the 1600’s, explained why the moon didn’t fall down on the Earth, by positing the laws of motion spanning both earthly and cosmic motions. The explanation of the moon’s continued elevation drops right out when one solves the differential equations for the motions of heavenly bodies. The contradiction between outer space and the earthly world, so vivid for earlier thinkers, falls away as if it had never existed.

Maxwell, in the 1800’s, resolved a number of peculiarities to do with electricity and magnetism, building on the conceptual and experimental work of Faraday and others, and positing a set of equations nearly as fundamental as Newton’s. But this leap in understanding lead to its own share of contradictions. Maxwell’s equations demonstrate that radio waves and all sorts of other waves are really just light waves at different frequencies, and that they all travel at the same speed – the speed of light – regardless of how fast the observer is moving. But this constancy of speed leads to mathematical contradictions in terms of Newtonian physics. Einstein’s theory of Special Relativity arose to deal with this contradiction, explaining how indeed it’s possible for all these waves to travel at the speed of light – by throwing out the commonsensical notion that the length, mass and time of objects are the same no matter how fast the person observing them is moving.

And Maxwell’s equations led to other problems as well, in the theory of heat. A hot object lets off electromagnetic radiation of many different frequencies, but if one adds up the energy of the radiation let off at different frequencies, one arrives at an infinite sum. Very bad. Max Planck, around the start of the 20’th century, had the answer: the energy is let off only in discrete chunks or “quanta,” not in a continuous range of values. With this humble act of contradiction-resolution quantum physics began. The simple idea of quantized energy led to a rapid-fire series of experimental and theoretical breakthroughs, similar to what we see today in molecular biology, and revealing the existence of a strange and unfamiliar world underlying the world observed every day, a world in which positions, momentums, energies and times are shifting and indeterminate rather than definite, in which particles can leap through solid barriers as long as they’re not being observed, in which particles can travel back through time.

While quantum theory was developing, Einstein was not only helping it along but also pushing in another direction. His Special Relativity theory frustrated him, because it directly contradicted Newton's theory of gravitation. Newtonian gravitational theory explained why the moon fails to fall in the sea, and how the planes move, but it came with a price: the unrealistic, clearly false assumption that grativational force moves from one object to another at infinite speed across great distances. Special Relativity says that nothing can move faster than the speed of light. To resolve this contradiction, the theory of General Relativity was conceived. The notion of spacetime, a 4-dimensional surface including three dimensions of space and one dimension of time was introduced, and in this context, gravity was explained as the curvature of spacetime. Massive objects curve spacetime, and then they move along paths in the spacetime continuum they have curved. This delicate feedback between objects and spacetime is captured in Einstein’s elegant but fabulously complex mathematics.

Gravity is a relatively weak force – you and I have only a very weak gravitational attraction between each other, for example. It only really kicks in for objects of large mass. This means that the difference between Newton’s and Einstein’s approaches to gravity isn’t really observable on the Earth in any simple way. But it is observable in outer space. General Relativity explained a previously baffling eccentricity in Mercury’s orbit. And it predicted that light coming from a star behind the sun, but near the edge of the sun from our perspective, would be slightly bent as it voyated toward us – a prediction that was validated by measurements done during a solar eclipse.

Making the Special Theory of Relativity consistent with quantum physics was not easy; this unification led to the theory of quantum electrodynamics (QED), a theory of the mid-20’th century that in many ways is the crown jewel of physics. QED is a complex and beautiful theory, commonsensically counterintuitive and yet fantastically pragmatic, predicting the observed mass of the electron, for example, to well over a dozen decimal places. There was no single superhero of QED: it was created by an international group of brilliant scientists such as Feynman, Tomonaga, Schwinger and Dirac, building on the mathematical quantum physics of earlier minds like Pauli, Schrodinger and Heisenberg. Laser physics is but a single example of the very numerous practical applications of QED.

QED grew into quantum field theory, which extends basic QED to give a fuller explanation of what happens inside the nuclei of particles. This is where the fascinating objects called “quarks” (a word drawn from Finnegan’s Wake) come into play. Quarks can never be observed in isolation, but in combinations they create particles like protons and neutrons. Understanding quarks helped us understand nuclei, but it required the use of whole new fields of mathematics, different from anything used for physics before. A class of theories called gauge theories or Yang-Mills theories was created, integrating all aspects of physical law except gravity. There are infinitely many Yang-Mills theories, but one has emerged as the best explanation of observed data; this is what’s called “the standard model.” Each different gauge theory potentially hypothesizes a different set of particles. The standard model postulates three families of quarks and leptons (e.g. the electron is a lepton), and also other mysterious entities called Higgs particles.

The standard model is not a simple thing. There are more than 20 parameters, whose values aren’t predicted by the theory. But by setting these 20 parameters, one gets an immense number of practical predictions. The theory is really quite a good one. The only problem is this little tiny thorn in its side called gravity. Einstein’s grand and beautiful vision of nonlinear feedback between matter and the spacetime continuum, doesn’t fit into the standard model picture of the cosmos at all. These two different theories explain different aspects of the shadows we see dancing on the wall, by making radically different postulates about the real world underlying the shadows. The two theories have to be brought together. That tall shadow can’t be both a tree blowing in the wind, and a tall creature moving about – there has to be a common explanation encompassing the data favoring each explanation.

And so the big question confronting theoretical physics these days is: How do you make gravity and the standard model play together? It’s thought that if we can answer this, we should be able to answer a bunch of other related questions. Simple things like: Where do the four forces we see come from? Why do we have the particles and waves that we have, instead of other ones? Why is space three dimensional and time one dimensional?

Physicists are a creative lot, and many potential answers to these questions have been proposed. Here I’ll discuss only two of them: superstring theory, which is perhaps the leading candidates in the physics establishment; and the universal computation approach, which is the domain of a handful of mavericks, but has an impressive philosophical simplicity and conceptual power.

Strings and Superstrings

The standard model of physics treats particles as points, as zero-dimensional objects. The particles may be blurred out over spacetime in that peculiar quantum way, but they’re still essentially points. This seems a reasonable approximation. But in the period 1968—1973, a number of physicists doing complex mathematical calculations regarding some advanced physics theories realized that, in fact, the math they were playing with implied a somewhat different model. What their physics equations were telling them was that particles aren’t points, they’re one-dimensional objects – strings, like violin strings.

Like QED, this work didn’t come out of any single genius scientist – there is no Einstein of strings. Edward Witten is most often mentioned as the leader of the string theory movement, but John Schwarz, Michael Green and many others have also made huge contributions. It has been observed that, in the early days, string theory was developed by middle-aged scientists because, according to the sociology of the physics community at the time, young scientists were too precarious in their careers to risk working on something as speculative as ten-dimensional harmonics. Nowadays of course, string theory is fairly mainstream, and it’s working on radical alternatives to string theory that’s more likely to get you denied tenure.

The strings these scientists found their equations were describing were very short strings – short as in 10^-33 centimeters. They’re so short that for almost all practical purposes, you can consider them as point particles. But for some things, like the unification of gravity and quantum physics, the stringiness of these little strings seemed to be important.

It’s important to understand the course that development took here. It wasn’t at all a matter of some kooky scientists sitting around and brainstorming about what the universe might be made of, and coming up with the idea that maybe particles are teeny-tiny violin strings. Rather, the mathematics of previous physics theories seemed to extend in a certain direction, and the most intuitive interpretation of this mathematics was in terms of vibrating strings. Once again, as in the birth of quantum physics itself, mathematics lead where common sense knew not how to tread.

Strings can be “open” like a violin string or “closed” like a rubber band. They move through spacetime they sweep out an imaginary surface called a “worldsheet.”

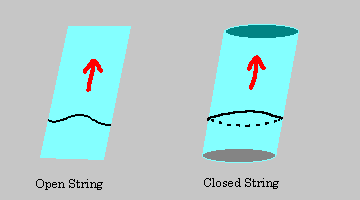
And the strings don’t just move – they vibrate. They vibrate in different modes, loosely similar to the harmonics or notes of the strings of a musical instrument. Physical parameters like mass, spin, and so forth, are mathematically derived from the vibrational modes of these tiny strings. Ultimately, in this view, there’s only one kind of object underlying every particle – the string. Different particles are just different modes of vibration of strings. A graviton, a gravity particle, is a particular kind of vibration of a closed string, and so on.

Strings interact with each other by splitting and joining, as in the following example:

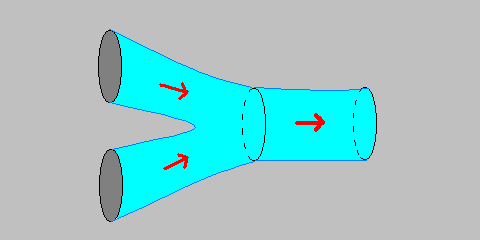
They can also be pinned to various objects, just as a violin string is pinned to the violin at both ends. Unlike violin strings, these tiny little physics strings can be pinned to objects of various dimensions, called D-branes. Much of string theory has to do with the study of D-branes, as well as strings themselves.

These are strings, but what about superstrings? What so super about them? To understand superstrings, you must understand that there are two basic types of particles in nature, named fermions and bosons (after 20’th century physicists Fermi and Bose). Fermions are “matter-ish” particles, like electrons, protons, neutrons, and quarks. Bosons are wispier things, like photons, gravitons, and W and Z particles. The standard model deals with both. In the mathematics of string theory, we find a certain kind of symmetry naturally arises: a symmetry between fermions and bosons. Fermions and bosons are groups together into collections called “supermultiplets” (hence the “super” in “supersymmetry”).

And here the mathematics yields the next big surprise. The only way to explain both fermions and bosons in string theory is to introduce supersymmetry, and the only way to make supersymmetry work in a logically consistent way, is to assume that the little strings exist in a 10 dimensional world. So, boom!, all of a sudden the real world producing the cave-wall shadows we see is ten dimensional, unlike the shadow-world we observe, which has three space dimensions and one time dimension. The idea of a higher-dimensional underlying spacetime wasn’t new to string theory – it was invented by Kaluza and Klein back in the early days of General Relativity. But back then it was one interesting speculation among others – now it was being pushed on physicists by complex mathematics that they barely understood.

How can it be that the real world is 10 dimensional whereas the observed world has three space dimensions and one time dimension? The standard explanation is a simple one: the extra six dimensions are curled up very small. Just as a two-dimensional piece of paper, rolled up small, looks like a one-dimensional line; so a ten-dimensional universe, rolled up small, can look like a four-dimensional universe. If the size of the rolled-up shape is around the same as the size of the strings themselves, then the extra 6 dimensions are almost impossible to observe, but the mathematics may still tell us they’re there.

It’s a fantastically surreal picture of the real world. In a very abstract, mathematical way, it seems to explain all four forces. Gravity, electromagnetism, and the weak and strong nuclear forces all come out of the same unifying equations – if you follow the mathematics and are willing to go with equations that render particles as vibrations of ten-dimensional strings.

But where’s the evidence that this isn’t all some kind of fabulous mathematical hallucination? Who says the universe really works this way? Where’s the proof?

There really isn’t any yet. Perhaps the most interest work drawing practical applications out of string theory involves black holes – regions of space with gravity so strong that any object that enters them, including light, can never escape. Black holes have mass, charge, and spin; and Stephen Hawking showed that they also radiate particles, because of complex effects in the vacuum around their boundaries. String theory has recently proved successful in explaining results in black hole theory, previously understood only in much more ad hoc, inelegant ways. Strominger and Vafa derived important equations about a certain class of black holes by describing them as 5-branes, 1-branes and open strings traveling down the 1-brane all wrapped on a 5-dimensional donut shape.

Of course, this branch of physics isn’t something that can very easily be experimented with – black holes are far away and are still mostly the domain of theory, although astronomers have identified a few. For more concrete implications of superstrings, we need to look elsewhere, perhaps in experiments physicists run in particle accelerators.

Remember, gravity is relevant for massive objects; but remember also Einstein’s discovery that mass and energy are two aspects of the same thing …

E=m c ²

When small particles are accelerated fast enough, they achieve very high energies, hence gravity applies to them significantly. The standard model integrates three forces: electromagnetism, and the weak and strong nuclear forces (two aspects of the physics that holds nuclei of atoms together). All these forces have about the same strength at energies of about 10¹⁶ gigavolts (GeV, a billion volts). It is estimated than when we get up to about 10¹⁹ GeV, gravity will join the party too, and all the forces will be about equally important. No existing particle accelerator can generate energies this high, but we’re creeping closer and closer. Unfortunately, the American superconducting supercollider project (SSC), which would have yielded about 20,000 GeV, was cancelled in favor of other scientific projects after being partially constructed. But it’s expected that around 2005, a European accelerator called the large hadron collider (LHC) will begin to operate at 8000 GeV per beam. We’re getting there.

Particle accelerator experiments should let us look for the supermultiplets, the fermion-boson groupings, that supersymmetry theories predict. Specifically, supersymmetry implies that every known elementary particle must have a "superpartner" particle. It is clear that no known particles are superpartners for each other. Where are the squarks corresponding to quarks, the selectrons corresponding to electrons, the gluinos corresponding to gluons, and so forth. It is hypothesized that the superpartners are so heavy you can only see them at very high energies. While this is quite reasonable and possible, one can understand why detractors call this a convenient excuse for maintaining a theory that postulates a huge number of particles no one has ever seen. Even if the LHC doesn’t reveal these particles, this won’t prove for sure that they don’t exist – they could just be even more massive than this machine would reveal. The problem is current mathematics of superstring theory doesn’t let us exactly predict superpartner mass, so we don’t know how big the accelerator would have to be to reveal the existence or otherwise of all these particles that the mathematics tells us should be there.

Although the creation of billion-dollar accelerators to test theories that are still not entirely quantitatively clear, is naturally a slow business, theoretical progress on superstrings progresses at a rapid pace. The period since 1994 has ground a second superstring theory revolution, in which new mathematical techniques have shown that what used to look like five different superstring theories, were actually just one mega-theory viewed from different perspectives. The march to unification moves on – on a mathematical level, with very little feedback from experimental data. The mathematical theories underlying different aspects of physics appear to unify more and more elegantly, if one’s willing to accept abstract mathematical structures like ten-dimensional vibrating strings and superpartner particles. But whether the universe agrees with this mathematics, or is stranger yet, remains to be seen. There is much history in physics to show that elegant mathematics can lead to empirically valid results. But this time, perhaps, have the mathematicians gone too far?

The Computational Universe

Superstring theory is just one among many approaches to unifying gravity and the standard model. It’s probably the most popular approach at present, and it does have a lot going for it. The mathematics is beautiful, and one result after another comes out, providing more and more evidence that the equations are sensible, yet providing no real quantitative predictions or solid empirical validation.

It’s not hard to see, however, why not all physicists accept the viability of the superstring approach. The problem isn’t so much that a universe of ten-dimensional vibrating strings is an absurd idea. Physicists are pragmatic as well as aesthetic, and will accept any hypothesis that seems to predict observed empirical data. The problem is that superstring theory doesn’t make any useful empirical predictions, and on the other hand, it postulates a huge number of particles that have never been seen. To go back to the Plato metaphor, it doesn’t tell us anything about how the shadows we see on the cave wall move. It predicts a whole lot of shadows we’ve never seen, though of course it’s possible we’ll see these shadows under some strange conditions that we haven’t encountered yet. What is does is to unify, conceptually and mostly mathematically, the most powerful and useful existing theories for explaining how shadows move.

Some of the alternatives, like loop theory, are worked out in almost as much detail as string theory, and by scientists with equally impressive pedigrees. And some of them are a bit more speculative and fringe-y. In the latter camp we find one of the more fascinating directions –the envisioning of the universe as a computer.

Unlike the string theorists, who have followed their mathematics wherever it leads and bent their intuitions to follow their math, the universe-as-computer folks are beginning with an intuition, and seeking to build appropriate mathematics around their intuition. Their intuition is a simple one: perhaps the universe is a giant computer. Computer programs, we have seen, can lead to fabulously complex behaviors. In fact there is mathematics suggesting that any system whatsoever can be represented as a computer program. So why not the universe itself?
:

One of the more vocal advocates of this point of view is Ed Fredkin, an eccentric multimillionaire who owns his own island and has been responsible for several innovations in computer science. Fredkin has been working for years on a model of the physical universe as a special kind of computer program called a “cellular automaton.” This is a reasonable choice, as cellular automata have been used to model all sorts of physical phenomena, from weather systems to immune systems to water flow in the ocean and neural networks in the brain. A cellular automaton consists of a collection of cells, each with a very simple program in it, which changes the cell’s state based on the state of other nearby cells.

Fredkin has gone a long way toward resolving various conceptual problems associated with the “universe as computer” idea. On the face of it, it’s not clear how quantum randomness and indeterminacy could come out of a computer program, or how the time-reversal that we see on the microscopic scale (particles can go back in time) could either. But Fredkin invented a whole new research area of reversible computing – it turns out that with enough memory available, computer programs can run both backwards and forwards. And he solved the quantum indeterminacy problem by introducing the seemingly oxymoronic notion of "unknowable determinism." Basically, he notes, if the universe is a computer that’s running at full blast and using all its resources to compute its own future as fast as possible, then there is no shortcut to predicting the future of this machine – there’s no way to build a faster computer than the universe itself. So if the universe is a computer, there’s no way to predict the future course of evolution of this computer, you just have to wait and see – in effect, from the point of view of particular observers like ourselves, the universal computer may be indeterminate.

But Fredkin, although he’s made a lot of progress, has not yet released his complete equations for the universe as a computer. One suspects there are difficult problems to crack here. Philosophically this approach is more appealing than string theory, but the mathematics doesn’t seem to roll out nearly as elegantly. And there are other competitors in this particular space who seem to be running up against similar walls. For instance, Stephen Wolfram, noted scientist and entrepreneur and founder of Mathematica Inc., has been working for years on a book describing a new theory of physics based on cellular automata. This has to be taken somewhat seriously since Wolfram himself set the direction for much of modern cellular automata research. But his book has been in preparation for years, and no one has seen exactly what he’s up to; how relevant his work will be to the dilemmas of quantum gravity remains to be seen.

Going even further out of the mainstream, Tony Smith, a maverick physicist in Georgia (who pays his rent as a criminal lawyer), has published a more complete computational physics theory than anyone else. His theory (the “D4-D5-E6-E7-E8 model”) is large and complex, presenting the universe as an 8-dimensional machine operating according to specific mathematical equations that he has articulated. Mainstream physicists like the superstringers have nothing but contempt for this kind of work. On the other hand, the amount of work that has gone into a theory like Smith’s is virtually nothing compared to the amount of work that has gone into superstrings, and from a bird’s-eye distance the results are not all that much less impressive. Smith’s theory runs into some subtle conceptual tangles in cases where superstring theory is clear and simple (for example, pion decay). On the other hand, Smith’s theory makes more concrete empirical predictions than superstring theory, a fact that has led Smith on an interesting excursion into the sociology of experimental science.

Specifically, the D4-D5-E6-E7-E8 model predicts that a particular kind of quark called the Top Quark should have a mass of about 130 GeV. On the other hand, the standard model predicts a mass around 170 GeV instead. Fermilab and other institutions have done experiments leading to numerical predictions of this mass, which should allow empirical selection between different theories like these. But when you get right down to it, what you find is that the interpretation of the empirical data is a very subtle matter. The estimation of quark mass is based on averaging values obtained over different “events” of observing various kinds of particles. But it’s not always clear when a particle has been observed – often experimental noise looks just the same as a particle observation. Whether quark mass comes out around 130 GeV or around 170 GeV turns out to depend on whether a few borderline cases are classified as particle observations or not. There’s a surprising amount of subjectivity here, right at the forefront of experimental physics, the hardest hard science on earth.

Whether Smith is right is not the point here – in all probability his theory has some interesting insights, but doesn’t capture the whole story. Perhaps it’s total bunk, perhaps it’s 90% of the way to the holy grail. Perhaps this theory, and superstrings, capture different aspects of the underlying truth. The point I want to make is that, even though this is hard empirical science, things are pretty much wide open at this point. The leading theory, superstrings, has virtually no empirical support, and is valued primarily because of the elegance of its mathematics. Indeed it was created almost entirely based on advanced mathematics rather than conventional physics. There are dozens of radically different theories, including conceptually fascinating ones like “the universe as a computer,” which exist at various stages of development. We don’t have the experimental tools to test these theories yet, and the tools that we have give results that are difficult to interpret, leading to potentially significant theoretical bias in the production of apparently hard experimental data. For advanced theoretical physics, this is a time of exciting exploration, not a time of solidity and stable continuous progress.

A Theory of Everything -- Not

So, let’s suppose the string theorists, or the universal computists, or some other group finally achieves their end goal -- unifying quantum theory and gravitation, creating one single equation, accounting in principle for all phenomena in the universe. What happens then? Do the angels descend from heaven, dancing and singing in the streets and on the rooftops, serving out the wine in holy grails laminated with spinning black holes, bringing peace on earth at long long last? More seriously: does science enter a whole new era, where every phenomenon observed is analyzed in terms of the one true equation?

Well, parts of physics will surely be revolutionized. There will be new technologies, maybe those we envision now like quantum gravity computers or time travel machines, maybe other types of things we can hardly imagine now. Perhaps, as some maverick theorists believe, new light will be shed on the mysteries of biological processes like cell development.

But no serious scientist really believes that such a “Theory of Everything” (TOE) in principle will really be a theory of everything in practice. There are a number of technical and conceptual points that will stop this from happening.

As superstring theorist John Schwarz says, “the TOE phrase is very misleading on several counts….. [And] it alienated many of our physics colleagues, some of whom had serious doubts about the subject anyway. Quite understandably, it gave them the impression that people who work in this field are a very arrogant bunch. Actually, we are all very charming and delightful.”

For one thing, if string theory or universal computation or some other approach succeeds in making quantum theory and gravitation play nice together, this still doesn’t explain why our universe is the way it is, because it doesn’t explain what physicists call the “initial conditions” of the universe: it only explains how things evolved from their starting-point. This may seem a small technical point but it’s a big one in practice: there may be many, many very different universes consistent with equations as general as those of string theory.

Next, we may find that one thing the “universal equation” binding quantum theory and gravitation teaches us is that some very important things can’t be explained or understood. Just as quantum theory has taught us that particles don’t have definite states, the next wave of physics may open up new kinds of indeterminacy and unknowability. We may wind up learning, in ever more exquisite detail, why our own finite, macroscopic minds are not up to the task of understanding the real world underlying the shadow-world they’ve evolved to see.

And this latter point ties in with the most serious problem with these approaches to physics: the problem of intractable calculations. Right now, the equations of string theory are so hard to solve that we can only really understand them in very special cases. There is an assumption that the mathematics of the next century will allow us to make more progress in this regard. But to what extent will this really be true? Right now, we can’t do explicit quantum theory calculations to understand proteins or neurons – only very simple molecules. And we can’t do string theory calculations to understand electrons and protons. To bring string theory to the next level, we’ll have to be able to use it to understand electrons and protons, but that may be as far as it goes – the elucidation of the implications of these micromicromicro-level equations for macroscopic phenomena may remain too difficult for mathematicians or computer-simulators to resolve for hundreds or thousands of years, or even forever.

It all comes down to Plato. From studying these shadows on the wall, we can’t really figure out what the birds and trees and squirrels are. But we can learn more and more about them. We can make deeper and deeper theories, some of them explaining the interaction of very small bits of shadow, some of them explaining particular kinds of large shadow. It’s vain to think we can fully understand reality, or even fully understand what “reality” means. The very notion of “everything,” when taken seriously, intrinsically goes beyond our understanding. The hubristic search to understand everything is valuable insofar as it give us the passion to understand more and more, but in more reflective moments, we have to acknowledge, as Schwarz did in the quote given above, that we can’t really capture the whole big universe in any little box -- not even a box composed of the most sophisticated and fantastic equations.